1-2星數學試題
- 問題求解
- 條件充分性判斷
打印試卷
問題求解
一個等腰梯形,上底是8,下底是12,底角45°,則此梯形面積( )
- A20
- B19
- C18
- D16
- E14
● 正確答案:A
收藏本題 糾錯
答案解析:
h=2,
S=(8+12)×2÷2=20 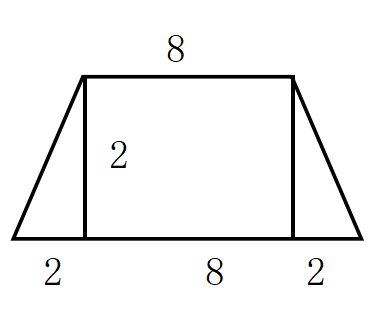
知識點:四邊形
已知不等式$a x ^ { 2 } + 5 x + c \geq 0$的解集為$- \frac { 1 } { 2 } \leq x \leq 3$,則a,c的值分別為( )。
- A$- \frac { 1 } { 3 } , - 2$
- B-2,3
- C$- \frac { 1 } { 2 } , 3$
- D2,3
- E-2,-3
● 正確答案:B
收藏本題 糾錯
答案解析:
令$a x ^ { 2 } + 5 x + c = 0$,則由題意,知方程的兩個根為$- \frac { 1 } { 2 } $,3.根據韋達定理,得$\left\lbrace\begin{array}{l} { - \frac { 1 } { 2 } + 3 = - \frac { 5 } { a } } \\ { - \frac { 1 } { 2 } \cdot 3 = \frac { c } { a } } \end{array}\right.$,所以$\left\lbrace\begin{array}{l} { a = - 2 } \\ { c = 3 } \end{array}\right.$
知識點:不等式
某商店本月的計劃銷售額為 20 萬元,由于開展了促銷活動,上半月完成了全月計劃的 60%,若全月要超額完成計劃的 25%,則下半月應完成銷售額( )萬元。
- A16
- B15
- C14
- D13
- E12
● 正確答案:D
收藏本題 糾錯
答案解析:
解析:$2 0 \times ( 1 + 0 . 2 5 ) - 2 0 \times 0 . 6 = 1 3$(萬元)
知識點:比例問題
某學生要邀請 8 位同學中的 4 位參加一項活動,其中甲、乙兩位同學要么都請,要么 都不請,共有( )種邀請方法。
- A24
- B26
- C28
- D30
- E32
● 正確答案:D
收藏本題 糾錯
答案解析:
分兩種情況進行討論。若甲乙都請,則共有$C _ { 6 } ^ { 2 } = 1 5$種方法,若甲乙都不請$C _ { 6 } ^ { 4 } = 1 5$,因此總共有30種方法。
知識點:排列組合
甲、乙二人同時同地沿一條公路前進,甲每小時走 8 千米,而乙第一小時走 1 千米,第二小時走 2 千米,第三小時走 3 千米,···,以后每走一小時都比前一小時多走 1 千米,那么經過( )小時后乙可以追上甲。
- A15
- B12
- C9
- D6
- E3
● 正確答案:A
收藏本題 糾錯
答案解析:
設經過 $x$ 小時后乙可以追上甲, 則根據題意有 $1+2+3+\cdots+x=8 x \Rightarrow \frac{(1+x) \cdot x}{2}=8 x$, 解得 $x=15$ 。
知識點:行程問題
已知某廠生產 $x$ 件產品的總成本為 $C=25000+200 x+\frac{1}{40} x^2$ (元), 要使平均成本最小, 所應生產的產品件數為 ( ) 件。
- A100
- B200
- C4000
- D1000
- E2000
● 正確答案:D
收藏本題 糾錯
答案解析:
根據題意, 知平均成本為 $\bar{C}=\frac{25000}{x}+200+\frac{1}{40} x$ 。那么根據算術平均值與幾何平均值的大小關系有 $\frac{25000}{x}+200+\frac{1}{40} x \geq 200+2 \cdot \sqrt{\frac{25000}{x} \cdot \frac{1}{40} x}$ 。
所以當且僅當 $\frac{25000}{x}=\frac{1}{40} x$, 即 $x=1000$ 時, 平均成本最小。
知識點:最值問題
若等差數列 $\left\{a_n\right\}$ 與等比數列 $\left\{b_n\right\}$ 滿足 $a_1=b_1=-1, a_4=b_4=8$, 則 $\frac{a_2}{b_2}$ 的值為 ( )。
- A5
- B4
- C3
- D2
- E1
● 正確答案:E
收藏本題 糾錯
答案解析:
由于 $a_4=a_1+3 d=-1+3 d=8 \Rightarrow d=3$, 所以 $a_2=a_1+d=-1+3=2$; 又 $b_4=b_1 \cdot q^3=-1 \cdot q^3=8 \Rightarrow q=-2$, 所以 $b_2=b_1 \cdot q=-1 \cdot(-2)=2$, 那么 $\frac{a_2}{b_2}=1$ 。
知識點:第五章 數列
已知圓$C _ { 1 } : x ^ { 2 } + y ^ { 2 } + 4 x - 4 y - 1 = 0$與圓$C _ { 2 } : x ^ { 2 } + y ^ { 2 } + 2 x - 1 3 = 0$的交點為 A,B,則 A,B 所在的直線方程為( )
- A$2 x - y + 6 = 0$
- B$2 x + y + 6 = 0$
- C$x - 2 y - 6 = 0$
- D$x - 2 y + 6 = 0$
- E$3 x - 2 y + 6 = 0$
● 正確答案:D
收藏本題 糾錯
答案解析:
$\left\lbrace\begin{array}{l} { x ^ { 2 } + y ^ { 2 } + 4 x - 4 y - 1 = 0 } \\ { x ^ { 2 } + y ^ { 2 } + 2 x - 1 3 = 0 } \end{array}\right.$$\Rightarrow 2 x - 4 y + 1 2 = 0 \Rightarrow x - 2 y + 6 = 0$
知識點:第八章 解析幾何
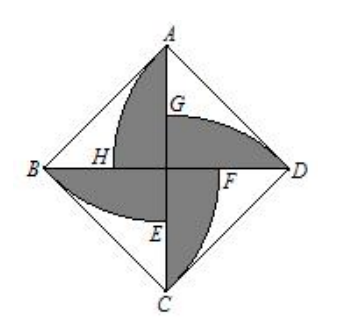
如圖所示, 正方形 $A B C D$ 的邊長為 1 米, 分別以 $A、B、C、D$ 為圓心, 1 米為半徑作弧 $BE$ 、弧 $CF$ 、弧 $DG$ 、弧 $AH$, 交 $AC$ 與 $E$ 和 $G$, 交 $BD$ 與 $F$ 和 $H$, 那么圖中陰影部分的面積為()平方米。
- A$\frac{\pi}{4}-\frac{1}{2}$
- B$2-\frac{\pi}{2}$
- C$\frac{\pi}{2}+1$
- D$\frac{\pi}{4}+\frac{1}{2}$
- E$\frac{\pi}{2}-1$
● 正確答案:E
收藏本題 糾錯
答案解析:
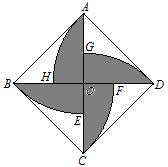
如圖所示, 知 $\angle A D H=45^{\circ}$, 且 $\triangle A O D$ 為等腰直角三角形, 所以 $A O=O D=\frac{\sqrt{2}}{2}$;
那么陰影部分的面積為 $S_{\text {陰 }}=4 \cdot\left(S_{\overline{A D H}}-S_{\triangle A O D}\right)=4 \cdot\left(\frac{1}{8} \pi \cdot 1^2-\frac{1}{2} \times \frac{\sqrt{2}}{2} \times \frac{\sqrt{2}}{2}\right)=\frac{\pi}{2}-1$ 。
知識點:第七章 幾何
若$2 ^ { a } = 8 ^ { b } = 6 4 ^ { c }$,$\frac { a - b - c } { a + b + c }$=( )
- A$\frac { 1 } { 3 }$
- B$\frac { 1 } { 2 }$
- C$\frac { 2 } { 3 }$
- D1
- E2
● 正確答案:A
收藏本題 糾錯
答案解析:
由$2 ^ { a } = 8 ^ { b } = 6 4 ^ { c }$得$2 ^ { a } = 2 ^ { 3 b } =2 ^ { 6 c } \Rightarrow a = 3 b = 6 c$$\Rightarrow \left\lbrace\begin{array}{l} { a = 6 c } \\ { b = 2 c } \end{array}\right.$$\frac { a - b - c } { a + b + c }$$= \frac { 6 c - 2 c - c } { 6 c + 2 c + c } = \frac { 3 c } { 9 c } = \frac { 1 } { 3 }$
知識點:第十一章 函數
兩個相同規格的容器,分別裝上A,B兩種液體后的總重量是1800克和1250克,已知A液體的重量是B液體的兩倍,那么這個空容器的重量是( )。
- A550克
- B600克
- C1100克
- D700克
- E1200克
● 正確答案:D
收藏本題 糾錯
答案解析:
設B溶液的重量為x克,空容器的重量為y克;則A溶液為2x克。則有$\left\lbrace\begin{array}{l} { 2 x + y = 1 8 0 0 } \\ { x + y = 1 2 5 0 } \end{array}\right.$$\Rightarrow \left\lbrace\begin{array}{l} { x = 5 5 0 } \\ { y = 7 0 0 } \end{array}\right.$
知識點:方程組問題
已知多項式$f ( x ) = x ^ { 3 } + a ^ { 2 } x ^ { 2 } + a x - 1$被x+1除余-2,則實數a的值為( )。
- A1
- B1或0
- C-1
- D-1或0
- E2
● 正確答案:B
收藏本題 糾錯
答案解析:
知識點:高次多項式的求值問題
有四個數,每三個數相加其和分別為22,24,27,20,則這四個數的平均值為( )
- A$\frac{27}{4}$
- B7
- C$\frac{15}{2}$
- D$\frac{31}{4}$
- E8
● 正確答案:D
收藏本題 糾錯
答案解析:
設這四個數的和為x,則這四個數分別為x-22,x-24,x-27,x-20,那么有x-22+x-24+x-27+x-20=x,解得x=31。所以這四個數的平均值為$\frac{x}{4} = \frac{31}{4}$。
知識點:平均值
若$log_{2}a+log_{\frac{1}{2}}b=2$,則$log_{a}4b$為( )
- A1
- B$\sqrt{2}$
- C$\frac{1}{2}$
- D2lg2
- Elg2
● 正確答案:A
收藏本題 糾錯
答案解析:
由$log_{2}a+log_{\frac{1}{2}}b=2$,可得$\log _ { 2 } a - \log _ { 2 } b = 2 \Rightarrow \log _ { 2 } \frac { a } { b } = 2 \Rightarrow \frac { a } { b } = 4 \Rightarrow a=4 b$,所以$log_{a}4b=log_{4b}4b=1$
知識點:冪函數、指數函數和對數函數
如圖所示,在三角形的每條邊上各有三個等分點,以這 9 個分點為頂點可畫出( )個三角形。

- A45
- B54
- C63
- D72
- E81
● 正確答案:E
收藏本題 糾錯
答案解析:
解析:三個點可以構成三角形的充要條件為三個點不在同一條直線,所以考慮總的取法減去三個點在同一直線上的情況即可。那么以這 9 個分點為頂點可畫出$N=C_{9}^{3}-3C_{3}^{3}=81$個三角形。
知識點:排列組合
已知集合$A=\left \{ 1,2,3,5,7,11 \right \}$,$B=\left \{ x\mid x^2-18x+45< 0 \right \}$,則$A\bigcap B$中元素的個數為( )。
- A3個
- B4個
- C5個
- D6個
- E0個
● 正確答案:A
收藏本題 糾錯
答案解析:
解析:根據題意,知$B=\left \{ x\mid 3< x< 15 \right \}$,那么$A\bigcap B=\left \{ 5,7,11 \right \}$,所以$A\bigcap B$中有3個元素。
知識點:不等式
已知球的外切正方體的體積$64\, \mathrm{cm}^3$為,則這個球的表面積為( )$\mathrm{cm}^2$.
- A$64\pi$
- B$62\pi$
- C$48\pi$
- D$38\pi$
- E$16\pi$
● 正確答案:E
收藏本題 糾錯
答案解析:
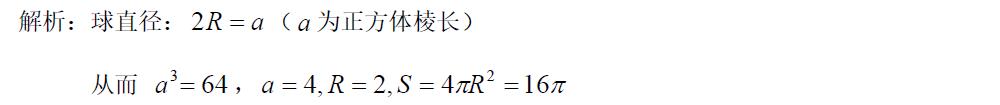
知識點:球體
a,b,c為質數,且a+b+c=16則a,b,c為邊的三角形為( )。
- A等邊三角形
- B等腰三角形
- C直角三角形
- D等腰直角三角形
- E不能構成三角形
● 正確答案:B
收藏本題 糾錯
答案解析:
知識點:實數及其運算
已知$x + \frac { 1 } { x } = 3$,則$x ^ { 2 } + \frac { 1 } { x ^ { 2 } }$,$x ^ { 3 } + \frac { 1 } { x ^ { 3 } }$,$x ^ { 4 } + \frac { 1 } { x ^ { 4 } }$的值依次為( )。
- A7,15,50
- B6,18,49
- C7,18,48
- D7,18,47
- E6,18,46
● 正確答案:D
收藏本題 糾錯
答案解析:
知識點:代數式的計算
已知5個人的平均年齡為29歲,且沒有小于24歲的,則這5個人中年齡的最大值不超過( )。
- A50
- B49
- C48
- D47
- E45
● 正確答案:B
收藏本題 糾錯
答案解析:
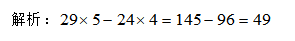
知識點:平均值
條件充分性判斷
直線 $A x+B y+C=0$ 必過圓 $O: 3 x^2+3 y^2-2 x-4 y-\frac{4}{3}=0$ 的圓心。
(1) $A+2 B+3 C=0$
(2) $A+2 B+C=0$
- A條件1充分,但條件2不充分;
- B條件2充分,但條件1不充分;
- C條件1和2單獨都不充分,但條件1和條件2聯合起來充分;
- D條件1充分,條件2也充分;
- E條件1和2單獨都不充分,條件1和條件2聯合起來也不充分;
● 正確答案:A
收藏本題 糾錯
答案解析:
解析: 根據題干, 圓心為 $\left(\frac{1}{3}, \frac{2}{3}\right)$, 所以有 $\frac{1}{3} A+\frac{2}{3} B+C=0$, 即有 $A+2 B+3 C=0$ 。
所以條件(1)充分, 但條件(2)不充分。
知識點:直線與圓位置關系
一件工作,甲先做 3 小時后,由乙接著做,則還需要 6 小時才可以完成。
(1)若甲單獨做需要 6 小時可以完成,乙單獨做需要 12 小時可以完成。
(2)若甲、乙單獨做都需要 9 小時可以完成。
- A條件1充分,但條件2不充分;
- B條件2充分,但條件1不充分;
- C條件1和2單獨都不充分,但條件1和條件2聯合起來充分;
- D條件1充分,條件2也充分;
- E條件1和2單獨都不充分,條件1和條件2聯合起來也不充分;
● 正確答案:D
收藏本題 糾錯
答案解析:
設甲先做 3 小時后, 由乙接著做還需要 $x$ 小時才可以完成。
由條件 (1),$\frac{1}{6} \times 3+\frac{1}{12} \times x=1 \Rightarrow x=6$ 。所以條件 (1) 充分。
由條件 (2), $\frac{1}{9} \times 3+\frac{1}{9} \times x=1 \Rightarrow x=6$ 。所以條件 (2) 也充分。
知識點:工程問題
$\frac{a}{a^2+7 a+1}=\frac{1}{10}$
(1) $a>0$
(2) $a^2+\frac{1}{a^2}=7$
- A條件1充分,但條件2不充分;
- B條件2充分,但條件1不充分;
- C條件1和2單獨都不充分,但條件1和條件2聯合起來充分;
- D條件1充分,條件2也充分;
- E條件1和2單獨都不充分,條件1和條件2聯合起來也不充分;
● 正確答案:C
收藏本題 糾錯
答案解析:
去 $\mathrm{a}=1$ 可知, 條件 (1) 不充分。條件 (2) 可知 $\left(a+\frac{1}{a}\right)^2=9, a+\frac{1}{a}=\pm 3$
$\frac{a}{a^2+7 a+1}=\frac{1}{a+7+\frac{1}{a}}$ 有兩個值, 所以條件 (2) 不充分。聯合條件 (1) 和條 件 (2) 可得到 $a+\frac{1}{a}=3$, 所以 $\frac{a}{a^2+7 a+1}=\frac{1}{a+7+\frac{1}{a}}=\frac{1}{10}$ 。
知識點:分式的代簡求值
燒杯中有純酒精溶液 $400 \mathrm{ml}$, 第一次倒出 $x \mathrm{ml}$ 后, 用水加滿, 在第二次再倒出同樣多的溶液, 再用水加滿, 則這時容器中酒精溶液的濃度為 $49 \%$ 。
(1) $x=120$
(2) $x=100$
- A條件1充分,但條件2不充分;
- B條件2充分,但條件1不充分;
- C條件1和2單獨都不充分,但條件1和條件2聯合起來充分;
- D條件1充分,條件2也充分;
- E條件1和2單獨都不充分,條件1和條件2聯合起來也不充分;
● 正確答案:A
收藏本題 糾錯
答案解析:
根據題意可列 $\frac{400-x-\frac{400-x}{400} \cdot x}{400}=49 \%$, 解得 $\mathrm{x}=120$ 或 $\mathrm{x}=680$ (舍).
知識點:溶液問題
可以確定每杯葡萄酒上漲了百分之幾
(1) 每杯葡萄酒上漲了0.5元
(2) 價格上漲后每杯7元
- A條件1充分,但條件2不充分;
- B條件2充分,但條件1不充分;
- C條件1和2單獨都不充分,但條件1和條件2聯合起來充分;
- D條件1充分,條件2也充分;
- E條件1和2單獨都不充分,條件1和條件2聯合起來也不充分;
● 正確答案:C
收藏本題 糾錯
答案解析:
條件(1)(2)單獨不充分,聯合知道原價為6.5元,上漲率為(7-6.5)/6.5,所以聯合充分
知識點:比例問題
方程$x^{2}-2mx+m^{2}-4=0$ 有兩個不相等的實根
(1)m>4
(2) m>3
- A條件1充分,但條件2不充分;
- B條件2充分,但條件1不充分;
- C條件1和2單獨都不充分,但條件1和條件2聯合起來充分;
- D條件1充分,條件2也充分;
- E條件1和2單獨都不充分,條件1和條件2聯合起來也不充分;
● 正確答案:D
收藏本題 糾錯
答案解析:
$\Delta =4m^{2}-4(m^{2}-4)=4m^{2}-4m^{2}+16>0$
所以無論m取何值,此方程永遠有兩個不等實根
知識點:方程實根分布問題
|a-b-c|+|b-c-a|-|c-a-b|=3c-a-b
(1)a,b,c分別為△ABC 的三邊長
(2)a,b,c為10以內的三個不同的質數,且均為奇數
- A條件1充分,但條件2不充分;
- B條件2充分,但條件1不充分;
- C條件1和2單獨都不充分,但條件1和條件2聯合起來充分;
- D條件1充分,條件2也充分;
- E條件1和2單獨都不充分,條件1和條件2聯合起來也不充分;
● 正確答案:D
收藏本題 糾錯
答案解析:
由條件(1),得|a-b-c|+|b-c-a|-|c-a-b|=-(a-b-c)-(b-c-a)+(c-a-b)=3c-a-b。所以條件(1)充分。
由條件(2),得a,b,c的數為3、5、7;那么|a-b-c|+|b-c-a|-|c-a-b|=-(a-b-c)-(b-c-a)+(c-a-b)=3c-a-b。所以條件(2)也充分。
知識點:絕對值
$a+b+c$一定為偶數.
(1)$a, b, c$為互不相同的合數
(2)$a, b, c$為互不相同的質數
- A條件1充分,但條件2不充分;
- B條件2充分,但條件1不充分;
- C條件1和2單獨都不充分,但條件1和條件2聯合起來充分;
- D條件1充分,條件2也充分;
- E條件1和2單獨都不充分,條件1和條件2聯合起來也不充分;
● 正確答案:E
收藏本題 糾錯
答案解析:

知識點:質數、合數和奇數、偶數
等差數列$\left \{ a_n \right \}$的前$100$項和$S_{100}=260$.
(1)公差$d=2$
(2)$a_1+a_3+\cdots +a_{99}=80$
- A條件1充分,但條件2不充分;
- B條件2充分,但條件1不充分;
- C條件1和2單獨都不充分,但條件1和條件2聯合起來充分;
- D條件1充分,條件2也充分;
- E條件1和2單獨都不充分,條件1和條件2聯合起來也不充分;
● 正確答案:C
收藏本題 糾錯
答案解析:

知識點:等差數列
$\frac{1}{1+x^2}+\frac{1}{1+y^2}=1$
(1)$xy=2$
(2)$xy=1$
- A條件1充分,但條件2不充分;
- B條件2充分,但條件1不充分;
- C條件1和2單獨都不充分,但條件1和條件2聯合起來充分;
- D條件1充分,條件2也充分;
- E條件1和2單獨都不充分,條件1和條件2聯合起來也不充分;
● 正確答案:B
收藏本題 糾錯
答案解析:
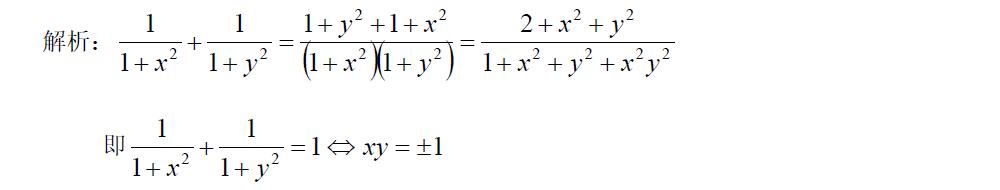
知識點:代數式的計算
開始做題