2024年5月第4周每日一練題目匯總
- 問題求解
- 條件充分性判斷
- 邏輯推理
打印試卷
問題求解
已知實數a,b滿足$| a + b | = 1 , | a ^ { 2 } - b ^ { 2 } | = 9$,則ab=
- A-3
- B-12
- C-20
- D20
- E12
● 正確答案:C
收藏本題 糾錯
答案解析:
知識點:絕對值
設$| a | < 1 , \quad | b | < 1$,則( )
- A| a + b | + | a - b | > 2
- B| a + b | + | a - b | = 2
- C| a + b | + | a - b | < 2
- D| a + b | + | a - b | ≥ 2
- E| a + b | + | a - b | ≤ 2
● 正確答案:C
收藏本題 糾錯
答案解析:
解法一,取$a = \frac { 1 } { 2 } , b = \frac { 1 } { 2 }$代入
解法二,$(| a + b | + | a - b | ) ^ { 2 }$$= 2 a ^ { 2 } + 2 b ^ { 2 } + 2 | a ^ { 2 } - b ^ { 2 } | =$$\left\lbrace\begin{array}{l} { 4 a ^ { 2 } , a ^ { 2 } \geq b ^ { 2 } } \\ { 4 b ^ { 2 } , a ^ { 2 } < b ^ { 2 } } \end{array}\right.$,從 而 有$| a + b | + | a - b | = 2 | a | < 2$或$| a + b | + | a - b | = 2 | b | < 2$
知識點:絕對值
甲、乙、丙三名射箭運動員在某次測試中各射擊20次,三人的測試成績如下表:
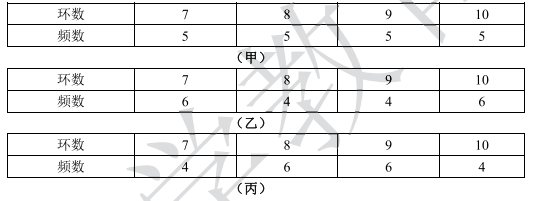
$S_{1},S_{2},S_{3}$分別表示甲、乙、丙三名運動員這次測試成績的方差,則有( ).
- A$S_{3}>S_{1}>S_{2}$
- B$S_{2}>S_{1}>S_{3}$
- C$S_{1}>S_{2}>S_{3}$
- D$S_{1}>S_{3}>S_{2}$
- E$S_{2}>S_{3}>S_{1}$
● 正確答案:B
收藏本題 糾錯
答案解析:
因為甲、乙、丙三名運動員測試成績的平均值都是8.5,方差表示數據的波動程度, 平均數相同,波動大方差大,三組數據乙的波動最大,甲次之,丙最小,所以選B.
知識點:平均值
設$|a|<1,|b|<1$,則( )
- A$|a+b|+|a-b|>2$
- B$|a+b|+|a-b|=2$
- C$|a+b|+|a-b|<2$
- D$|a+b|+|a-b|\geq 2$
- E以上答案均不正確
● 正確答案:C
收藏本題 糾錯
答案解析:
解法一,取$a=\frac{1}{2},b=\frac{1}{2}$代入。
解法二,$\left ( |a + b| + | a - b | \right ) ^ { 2 } = 2 a ^ { 2 } + 2 b ^ { 2 } + 2 | a ^ { 2 } - b ^ { 2 } | =\left\lbrace\begin{array}{l} { 4 a ^ { 2 } , a ^ { 2 } \geq b ^ { 2 } } \\ { 4 b ^ { 2 } , a ^ { 2 } < b ^ { 2 } } \end{array}\right.$
從而有
$| a + b | + | a - b | = 2 | a | < 2 $
或
$|a + b | + | a - b | = 2 | b | < 2$
知識點:三角不等式
$| 2 x - a | \leq 1 , \quad | 2 x - y | \leq 1$,則$| y - a |$的最大值是( )
- A1
- B3
- C2
- D4
- E5
● 正確答案:C
收藏本題 糾錯
答案解析:
$| y - a | = | ( 2 x - a ) - ( 2 x - y ) | \leq | 2 x - a | + | 2 x - y | \leq 1 + 1 = 2$
知識點:三角不等式
有四個數,每三個數相加其和分別為22,24,27,20,則這四個數的平均值為( )
- A$\frac{27}{4}$
- B7
- C$\frac{15}{2}$
- D$\frac{31}{4}$
- E8
● 正確答案:D
收藏本題 糾錯
答案解析:
設這四個數的和為x,則這四個數分別為x-22,x-24,x-27,x-20,那么有x-22+x-24+x-27+x-20=x,解得x=31。所以這四個數的平均值為$\frac{x}{4} = \frac{31}{4}$。
知識點:平均值
已知5個人的平均年齡為29歲,且沒有小于24歲的,則這5個人中年齡的最大值不超過( )。
- A50
- B49
- C48
- D47
- E45
● 正確答案:B
收藏本題 糾錯
答案解析:
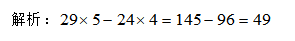
知識點:平均值
條件充分性判斷
5,8,$x$,10,4的方差是6.8.
(1)這組數據的平均數是$2x$.
(2)$x=3$.
- A條件(1)充分,但條件(2)不充分.
- B條件(2)充分,但條件(1)不充分.
- C條件(1)和(2)單獨都不充分,但是條件(1)和(2)聯合起來充分.
- D條件(1)充分,條件(2)也充分.
- E條件(1)和(2)單獨都不充分,聯合起來也不充分.
● 正確答案:D
收藏本題 糾錯
答案解析:
$\frac { 5 + 8 + x + 1 0 + 4 } { 5 } = 2 x \Rightarrow x = 3$,進而可得$S ^ { 2 } = \frac { ( 5 - 6 ) ^ { 2 } + ( 8 - 6 ) ^ { 2 } + ( 3 - 6 ) ^ { 2 } + ( 1 0 - 6 ) ^ { 2 } + ( 4 - 6 ) ^ { 2 } } { 5 } = 6 . 8$,故兩條件都充分.
知識點:平均值
已知X,y是正數,則能確定它們的幾何平均值。
(1)x,y的算術平均值為6
(2)$\frac { 1 } { x } + \frac { 1 } { y } = 4$
- A條件1充分,但條件2不充分;
- B條件2充分,但條件1不充分;
- C條件1和2單獨都不充分,但條件1和條件2聯合起來充分;
- D條件1充分,條件2也充分;
- E條件1和2單獨都不充分,條件1和條件2聯合起來也不充分;
● 正確答案:C
收藏本題 糾錯
答案解析:

知識點:平均值
若 $a 、 b 、 c$ 的算術平均值是 $\frac{7}{3}$, 則幾何平均值是 2 。
(1)$a 、 b 、 c$ 是滿足 $a>b>c>0$ 的三個整數, $b=2$
(2)$a 、 b 、 c$ 是滿足 $a>b>c \geq 1$ 的三個整數, 且 $a, b$ 為方程 $x^2-p x+8=0$ 的兩根
- A條件1充分,但條件2不充分;
- B條件2充分,但條件1不充分;
- C條件1和2單獨都不充分,但條件1和條件2聯合起來充分;
- D條件1充分,條件2也充分;
- E條件1和2單獨都不充分,條件1和條件2聯合起來也不充分;
● 正確答案:D
收藏本題 糾錯
答案解析:
解析: 由條件 (1), $a>b>c>0$ 為整數, 且 $b=2$, 所以 $c=1$; 又 $a 、 b 、 c$ 的算術平均值是 $\frac{7}{3}$, 所以 $a=4$ 。即 $\sqrt[3]{a b c}=2$, 所以條件(1)充分。
由條件(2), $a b=8=8 \times 1=4 \times 2$, 且 $a>b>c \geq 1$ 為整數; 則有 $a=4, b=2$ 。又 $a 、 b 、 c$ 的算術平均值是 $\frac{7}{3}$, 所以 $c=1$ 。即 $\sqrt[3]{a b c}=2$, 所以條件(2)也充分。
知識點:平均值
不等式$\left|x+\log _3 x\right|<|x|+\left|\log _3 x\right|$
(1) $x>0$
(2) $x<1$
- A條件1充分,但條件2不充分;
- B條件2充分,但條件1不充分;
- C條件1和2單獨都不充分,但條件1和條件2聯合起來充分;
- D條件1充分,條件2也充分;
- E條件1和2單獨都不充分,條件1和條件2聯合起來也不充分;
● 正確答案:C
收藏本題 糾錯
答案解析:
取 $x=1, x=0$, 則知條件(1)和條件(2)都不充分。 聯合條件(1)和條件(2)
$|a+b|<|a|+|b| \Leftrightarrow a b<0$,即 $ x \log _3 x<0$,即 $0<x<1$
知識點:絕對值
已知 $x < 0 < z,
xy > 0$, 則 $|x+z|+|y+z|-|x-y|=0$(1) $|y|>|z|>|x|$
(2) $|x|>|z|>|y|$
- A條件1充分,但條件2不充分;
- B條件2充分,但條件1不充分;
- C條件1和2單獨都不充分,但條件1和條件2聯合起來充分;
- D條件1充分,條件2也充分;
- E條件1和2單獨都不充分,條件1和條件2聯合起來也不充分;
● 正確答案:D
收藏本題 糾錯
答案解析:
顯然 $x<0, y < 0,
z >0$ 。由條件 (1) $|y|>|z|>|x|$ 可得: $x+z>0, y+z<0$,$x-y>0$ 。因此 $|x+z|+|y+z|-|x-y|=x+z-y-z-(x-y)=0$, 條件 (1) 充分。
由條件 (2) $|x|>|z|>|y|$ 可得: $x+z < 0,
y+z > 0, x-y < 0$因此 $|x+z|+|y+z|-|x-y|=-x-z+y+z+(x-y)=0$, 條件(2)也充分。
知識點:絕對值
可確定$x+y$的最大值與最小值.
(1)$ |x+2|+|y-5|=4$
(2)$|1-x|+|y+1|=5$
- A條件(1)充分,但條件(2)不充分.
- B條件(2)充分,但條件(1)不充分.
- C條件(1)和條件(2)單獨都不充分,但條件(1)和條件(2)聯合起來充分.
- D條件(1)充分,條件(2)也充分.
- E條件(1)和條件(2)單獨都不充分, 條件(1)和條件(2)聯合起來也不充分.
● 正確答案:D
收藏本題 糾錯
答案解析:
條件(1)和條件(2)所圍成的區域均為正方形,故可以確定$x+y$的最大值與最小值.
知識點:絕對值方程
$|x-y|\leq 2$
(1)$|x-a|\leq 1$
(2)$|y-a|\leq 1$
- A條件1充分,但條件2不充分;
- B條件2充分,但條件1不充分;
- C條件1和2單獨都不充分,但條件1和條件2聯合起來充分;
- D條件1充分,條件2也充分;
- E條件1和2單獨都不充分,條件1和條件2聯合起來也不充分;
● 正確答案:C
收藏本題 糾錯
答案解析:

知識點:三角不等式
$a=b=c$。
(1) $a, b, c$ 的平均數為 0
(2) $a, b, c$ 的方差為 0
- A條件1充分,但條件2不充分;
- B條件2充分,但條件1不充分;
- C條件1和2單獨都不充分,但條件1和條件2聯合起來充分;
- D條件1充分,條件2也充分;
- E條件1和2單獨都不充分,條件1和條件2聯合起來也不充分;
● 正確答案:B
收藏本題 糾錯
答案解析:
由條件 (1), $\frac{a+b+c}{3}=0 \Rightarrow a+b+c=0$, 無法確定 $a=b=c$, 所以條件 (1) 不充分。
由條件 (2), 設 $a, b, c$ 的平均數為 $\bar{x}$, 那么有 $\frac{1}{3}\left[(a-\bar{x})^2+(b-\bar{x})^2+(c-\bar{x})^2\right]=0$,
即 $a=b=c=\bar{x}$ 。所以條件 (2) 充分。
知識點:平均值
邏輯推理
通過最近幾年的市場調研報告可以得出一個結論,一家教育機構要想獲得市場份額,必須全面提升服務水平。同時,只有發現并理解客戶的需求,才能全面提升服務水平。
根據上述信息,以下哪些為真?
(1)一個獲得市場份額的教育機構可能沒理解客戶需求。
(2)除非全面提升服務水平,否則獲得市場份額就是一句空話。
(3)如果發現了客戶需求,就能確保全面提升服務水平。
- A(2)。
- B(1)(3)。
- C(2)(3)。
- D(1)(2)(3)。
- E都不符合。
● 正確答案:A
收藏本題 糾錯
答案解析:
解析:題干為 獲得市場份額→全面提升服務水平→發現且理解客戶需求。
對于(1)一個獲得市場份額的教育機構可能沒理解客戶需求。是題干的矛盾關系。注意假言P→Q與P且非Q互為矛盾關系。
對于(2),除非A否則B為非B推A,所以(2)為獲得市場份額→全面提升服務水平。符合題干。
對于(3)肯定后件的支判斷中的一部分,無法推出前件。
知識點:假言判斷(命題)
根據城鎮北京國際城市發展研究院最近發布首部《社會管理藍皮書》,2020年城市有近4.5億人的流動人口。再來看樓市現狀,存量房已有3.5億套。可是這卻絲毫不影響某些核心城市核心地段的核心樓盤。近期某樓市開盤依舊火爆,甲乙丙丁相約有意買房。已知:
(1)如果甲買房,則乙一定買房。
(2)只有丙不買房,乙才買房。
(3)只有丁拿到折扣,甲才買房。
(4)如果丁拿到折扣,則丙一定買房。
根據上述,以下哪項一定也為真?
- A甲買房,丙沒有買房。
- B甲沒有買房,乙和丁買房。
- C甲乙丙是否買房,不能確定。
- D甲沒有買房,乙和丙不確定。
- E甲買房,丁拿到折扣。
● 正確答案:D
收藏本題 糾錯
答案解析:
解析:結合條件(2)(3)(4),可知:(5)甲買房→丁拿到折扣→丙買房→乙不買房。再結合(1)(5)根據歸謬法(已知:P→Q,﹁P→Q,可以推知Q恒成立),得甲不買房。其余無法確定。
知識點:假言判斷(命題)
三位期貨專家正在對三家上市公司明天的期貨走勢進行預測:
章姍說:“糧食板塊的期貨會有一些上升,但不能期望過高。”
李斯說:“鋼鐵板塊的期貨可能下跌,除非糧食板塊的期貨上升超過5%。”
王武說:“如果鋼鐵板塊的期貨上升,畜牧業板塊的期貨也會上升。”
三位期貨專家預測的后一天證明他們的預言都對,而且畜牧業板塊的期貨跌了。
以下哪項敘述最可能是那一天期貨變動的情況?
- A糧食板塊期貨上升了9%,鋼鐵板塊期貨上升了4%。
- B糧食板塊期貨上升了7%,鋼鐵板塊期貨下跌了3%。
- C糧食板塊期貨上升了4%,鋼鐵板塊期貨上升了2%。
- D糧食板塊期貨上升了5%,煤炭板塊期貨持平。
- E糧食板塊期貨上升了2%,鋼鐵板塊期貨有所上升。
● 正確答案:B
收藏本題 糾錯
答案解析:
【假言判斷】已知畜牧業板塊的期貨下跌,否定了王武說的話的后件,由此可推出王武的前件也為假,即鋼鐵板塊的期貨沒有上升。據此排除A、C、E三項。而D項說的是煤炭板塊,是無中生有,因此可以排除。若B項為真,三人說話都為真,符合題干. 當選。
知識點:假言判斷(命題)
上個世紀80年代流行去舞廳跳舞,如果“福泰”娛樂廳在同一天既開放交誼舞廳又開放迪斯科舞廳,那么它也一定開放保齡球廳。該娛樂廳星期二不開放保齡球廳,小趙只有當開放交誼舞廳時才去“福泰”娛樂廳。
如果上述斷定是真的,那么以下哪項也一定是真的?
- A星期二小趙不會光顧“福泰”娛樂廳。
- B小趙不會在同一天在“福泰”娛樂廳既光顧交誼舞廳又光顧迪斯科舞廳。
- C“福泰”娛樂廳在星期二不開放迪斯科舞廳。
- D“福泰”娛樂廳只在星期二不開放交誼舞廳。
- E如果“福泰”在星期二開放交誼舞廳,那么這天它一定不開放迪斯科舞廳。
● 正確答案:E
收藏本題 糾錯
答案解析:
【考點:假言、聯言判斷】解析:交誼舞廳∧迪斯科→保齡=﹁保齡→﹁交誼舞廳∨﹁迪斯科=交誼舞廳∧﹁保齡→﹁迪斯科;星期二→﹁保齡;小趙去福泰→交誼舞廳。將五個項依次驗證,發現E項一定為真。
知識點:假言判斷(命題)
上個世紀80年代流行去舞廳跳舞,如果“福泰”娛樂廳在同一天既開放交誼舞廳又開放迪斯科舞廳,那么它也一定開放保齡球廳。該娛樂廳星期二不開放保齡球廳,小趙只有當開放交誼舞廳時才去“福泰”娛樂廳。
如果題干的斷定是真的,并且事實上小趙星期二光顧“福泰”娛樂廳,則以下哪項一定是真的?
- A“福泰”在小趙光顧的那天沒開放迪斯科舞廳。
- B“福泰”在小趙光顧的那天沒開放交誼舞廳。
- C“福泰”在小趙光顧的那天開放了保齡球廳。
- D“福泰”在小趙光顧的那天既開放了交誼舞廳,又開放了迪斯科舞廳。
- E“福泰”在小趙光顧的那天既沒開放交誼舞廳,又沒開放迪斯科舞廳。
● 正確答案:A
收藏本題 糾錯
答案解析:
【考點:假言判斷,聯言判斷】小趙星期二光顧了“福泰”娛樂廳,即星期二這天交誼舞廳開放了,根據上一題的第一個推理式得到:迪斯科舞廳肯定沒有開放。
知識點:假言判斷(命題)
春暉養老院開展了豐富多彩的娛樂活動,通過對老人的幾個愛好調查發現,在麻將、象棋、紙牌等娛樂項目中,某養老院的老人都喜歡和打麻將的老人玩,而不喜歡和玩紙牌的老人玩。已知4位老人中,甲是該養老院的老人,乙不愛打麻將,丙愛打麻將,丁不愛玩紙牌。根據以上陳述,以下各項可能為真,除了哪項?
- A甲喜歡和乙玩。
- B甲不喜歡和乙玩。
- C甲不喜歡和丙玩。
- D甲不喜歡和丁玩。
- E甲喜歡和丁玩。
● 正確答案:C
收藏本題 糾錯
答案解析:
【考點:有效信息匹配,直言判斷】解析:丙愛麻將,根據題干條件,甲會喜歡和丙玩,因此C一定假。A選項,假設乙喜歡象棋,但題干沒有說甲是否喜歡和象棋愛好者玩,所以A均可能為真,可能為假。
對于乙,不知道乙是否喜歡玩紙牌,如果喜歡紙牌則選項B正確,不喜歡紙牌則B不能判斷。同理可證D、E(不知道甲是否還喜歡和其他愛好者玩,比如象棋等。也不知道丁是否愛麻將)
知識點:假言判斷(命題)
在本年度足球聯賽中,莫妮卡隊主教練發現,東東隊5名主力隊員子、丑、寅、卯、辰之間的上場配置有如下規律:
I.若子上場,則丑也要上場。
Ⅱ.只有子不上場,寅才不上場。
Ⅲ.要么寅不上場,要么丑和辰中有人不上場。
Ⅳ.除非寅不上場,否則卯上場。
若丑不上場,則以下哪項配置合乎上述規律?
- A子、丑、寅同時上場。
- B寅不上場,卯、辰同時上場。
- C子不上場,寅、卯都上場。
- D子、卯都上場,辰不上場。
- E子、卯、辰都不上場。
● 正確答案:C
收藏本題 糾錯
答案解析:
【考點:假言判斷復合推理】題干條件整理如下:
①子上場→丑上場=﹁丑上場→﹁子上場;
②子上場→寅上場;
③要么﹁寅上場,要么(﹁丑上場∨﹁辰上場);
④寅上場→ 卯上場
⑤﹁丑上場。
有⑤和①可得﹁子上場,有⑤和③可得寅上場,再由④可得卯上場,辰不能確定。故選C。
知識點:假言判斷(命題)
東北人大飯店如果有鍋包肉或者有溜肉段,則必然會有小雞燉蘑菇;飯店在初十五不會賣小雞燉蘑菇;只有當東北人大飯店賣溜肉段時,大劉才會與朋友到東北人大飯店吃海鮮。 如果上述斷定為真,以下哪項一定為真?
- A東北人大飯店在初十五不會賣鍋包肉。
- B大劉與朋友到東北人大飯店不會既吃鍋包肉,又吃溜肉段。
- C東北人大飯店只有在初十五才不賣溜肉段。
- D大劉不會在初十五與朋友到東北人大飯店吃海鮮,因為那里沒有小雞燉蘑菇。
- E如果大劉在初十五與朋友到東北人大飯店吃海鮮,他們肯定吃得到鍋包肉。
● 正確答案:A
收藏本題 糾錯
答案解析:
解析:(1)鍋包肉或者溜肉段→小雞燉蘑菇;(2)初十五→﹁小雞燉蘑菇;(3)吃海鮮→溜肉段;(1)(2)聯合可知:初十五→﹁鍋包肉且﹁溜肉段(4);將選項結合題干可知,B、C、D、E無法從題干中推出,A正確。注意,D項的因果關系不能有題干的條件關系得出。
知識點:假言判斷(命題)
廣越地區某主干道的上下班高峰期堵車現象極為嚴重,原因是紅綠燈轉換時間不合理,往往導致車輛不能持續有序前行。為緩解該現象,相關部門對該主干道上的6個紅綠燈(編號1號、2號、3號、4號、5號、6號)重新設置了時間,其中滿足下面條件:
(1)如果3號是綠燈,則4號也要是綠燈;
(2)只有1號是紅燈,2號才能是紅燈;
(3)2號和4號不能同時是綠燈,也不能同時是紅燈;
(4)如果5號和6號同時是綠燈,則3號也要是綠燈。
如果現在1號和6號是綠燈,并且在無需考慮黃燈的參與,下面哪項一定為真的是?
- A2號和5號是綠燈。
- B2號和3號是綠燈。
- C2號和5號是紅燈。
- D4號綠燈,5號紅燈。
- E2號綠燈,5號紅燈。
● 正確答案:E
收藏本題 糾錯
答案解析:
(1)3綠→4綠;(2)2紅→1紅;
(3)2、4必須一紅一綠;(4)5綠且6綠→3綠;
依1綠代入(2)知非2紅,即2綠(a);a代入(3)知4紅(b),b代入(1)知道非3綠(c),代入(4)得(非5綠)或(非6綠),又根據已知6綠,得到非5綠,即5紅。因此E選項正確。
知識點:假言判斷(命題)
“功成名就”出自《墨子·修身》:“功成名遂,名譽不可虛假。”近期,研究者發現:一個人如果功成名就,則他有能力或具備運氣成分。下列哪項對研究者的觀點起到了質疑作用?
- A甲功成名就,但他沒有能力,也沒有具備運氣成分
- B乙沒有功成名就,但他有能力且具備運氣成分
- C丙沒有功成名就,他沒有能力,也沒有具備運氣成分
- D丁功成名就,則他有能力且具備運氣成分
- E戊功成名就,但沒有能力
● 正確答案:A
收藏本題 糾錯
答案解析:
題干:(功成名就)p→(能力∨運氣)q。對p→q起到質疑作用的是(p ∧﹁q),A正確。
知識點:假言判斷(命題)
NBA新賽季很快到來,但是依然有很多球員還沒找到一份合同,其中就包括馬修思。這位老將至今沒有等到合同,甚至連老將底薪都沒有。馬修思如今已經35歲,還經歷過重傷,想繼續拿到NBA合同已經很難,也許他的生涯也到了終點。NBA湖某隊董事會在某賽季前商討,得出結論為,如果選擇馬修思,就不能選擇杜蘭特。
以下哪項與題干結論一致?
- A如果不選擇杜蘭特,就選擇馬修思
- B不能兩人都選擇
- C不能兩人都不選擇
- D只有選擇杜蘭特,才選擇馬修思
- E除非選擇馬修思,否則不選擇杜蘭特
● 正確答案:B
收藏本題 糾錯
答案解析:
馬修思→不杜蘭特=不馬修思或不杜蘭特=不(馬修思且杜蘭特),即B.不能兩人都選擇。
知識點:假言判斷(命題)
某大學擬從多名學生中選取2名優秀的雙打乒乓球運動員代表學校參加聯賽,配備的隊服共有藍色和紅色兩種顏色。且(1)若甲和乙一起上場,則穿紅色隊服;(2)若甲和丙一起上場,則穿紅色隊服;(3)若甲和丁一起上場,則穿藍色隊服。
現在已知今天甲和另一名同學組隊上場,穿的是藍色隊服,則以下為真的是?
- A該名同學是乙或丙
- B該名同學是乙
- C該名同學是丁
- D該名同學不是丙
- E該名同學不是丁
● 正確答案:D
收藏本題 糾錯
答案解析:
1)甲乙→紅;(2)甲丙→紅;(3)甲丁→藍。現在已知甲與某同學穿藍色,因此不是乙、不是丙,D符合結果。是否是丁則無法判斷。
知識點:假言判斷(命題)
2018年首次開啟的世界排球聯賽(VOLLEYBALL NATIONS LEAGUE,縮寫VNL),前身是1993年開始的世界女排大獎賽,我國一直占有強大優勢,經調研發現,某國五名主力隊員之間的上場有如下規律安排:
(1)若甲上場,則乙也要上場:
(2)只有甲不上場,丙才不上場;
(3)要么丙不上場,要么乙和戊中有人不上場。
(4)若乙上場,則丙、戊都上場。
(5)除非丙不上場,否則丁上場。
若該國五名主力最多有兩人上場,以下哪項配置合乎上述規律?
- A甲、丙同時上場
- B丙不上場,丁、戊同時上場
- C甲不上場,丙、丁都上場
- D甲、丁都上場,戊不上場
- E甲、丁、戊都不上場
● 正確答案:C
收藏本題 糾錯
答案解析:
根據結合(4)假設乙上場,則丙、戊都上場,恰有三人上場,與已知五名主力最多有兩人上場相矛盾,因此假設不成立,乙不上場(a);a代入(1)可知甲不上場(b);a結合(3)知丙上場(b),b代入(5)知丁上場。因此C正確。
知識點:假言判斷(命題)
電影《寂靜之地》講述了末日一家人帶著幸存的兩個孩子來到鄉下躲避沒有視覺但聽覺靈敏的怪物,一家人用手語交流每天在小心翼翼中度日生活,最終女兒發現借助擴音器擊敗怪物的故事。因此,可以得出的結論是:怪物被擊敗,除非擴音器失靈。
以下斷定中與上述結論含義相同的是:
(1)如果擴音器失靈,則怪物不會被擊敗。
(2)如果怪物被擊敗,則擴音器沒有失靈。
(3)如果擴音器沒有失靈,則怪物被擊敗。
- A(1)
- B(2)(3)
- C(1)(3)
- D(3)
- E(1)(2)(3)
● 正確答案:D
收藏本題 糾錯
答案解析:
(A,除非B=﹁A→B=﹁B→A)解析:怪物被擊敗,除非擴音器失靈即:擴音器不失靈→怪物被擊敗,也可以寫成:怪物不被擊敗→擴音器失靈。因此(3)正確。
知識點:假言判斷(命題)
電影《寂靜之地》講述了末日一家人帶著幸存的兩個孩子來到鄉下躲避沒有視覺但聽覺靈敏的怪物,一家人用手語交流每天在小心翼翼中度日生活,最終女兒發現借助擴音器擊敗怪物的故事。因此,可以得出的結論是:怪物被擊敗,除非擴音器失靈。
在以下所列情況中,表明題干斷定為假的是:
(1)擴音器沒有失靈,并且怪物被擊敗。
(2)擴音器沒有失靈,并且怪物沒有被擊敗。
(3)擴音器失靈,并且怪物被擊敗。
- A(1)
- B(2)
- C(3)
- D(2)(3)
- E(1)(2)(3)
● 正確答案:B
收藏本題 糾錯
答案解析:
解析:怪物被擊敗,除非擴音器失靈即:擴音器不失靈p→怪物被擊敗q,負命題p且非q是“擴音器不失靈且怪物不被擊敗”,因此(2)正確。
知識點:假言判斷(命題)
開始做題