4星數學試題
- 問題求解
- 條件充分性判斷
打印試卷
問題求解
已知a,b,c為實數,且多項式$x3+ax^{2}+bx+c$能被$x^{2}+3x-4$整除,則$2a-2b-c=$( )。
- A14
- B15
- C12
- D13
- E11
● 正確答案:A
收藏本題 糾錯
答案解析:
解析:根據題意,設$f(x)=x^{3}+ax^{2}+bx+c=(x^{2}+3x-4).q(x)$$= ( x + 4 ) ( x - 1 ) \cdot q ( x )$,則有$\left\lbrace\begin{array}{l} { f ( 1 ) = 1 + a + b + c = 0 } \\ { f ( - 4 ) = ( - 4 ) ^ { 3 } + 1 6 a - 4 b + c = 0 } \end{array}\right.$$\Rightarrow \left\lbrace\begin{array}{l} { b = 3 a - 1 3 } \\ { c = 1 2 - 4 a } \\ \end{array}\right.$,所以$2 a - 2 b - c = 1 4$
知識點:第三章 整式與分式
已知長方形的長是寬的2倍,且周長為2,將這個長方形繞其寬旋轉一周,則所得圓柱體的體積為( )。
- A$\frac { \pi } { 2 7 }$
- B$\frac { 4\pi } { 9 }$
- C$\frac { 4\pi } { 27 }$
- D$\frac { \pi } { 9 }$
- E$\frac { 2\pi } { 27 }$
● 正確答案:C
收藏本題 糾錯
答案解析:
設長方形的寬為X,則長為2X。根據題意,有$x + 2 x = 1 \Rightarrow x = \frac { 1 } { 3 }$,那么所得底面半徑為$\frac{2}{3}$,高為$\frac{1}{3}$的圓柱,所以圓柱體的體積為$V = \pi \cdot ( \frac { 2 } { 3 } ) ^ { 2 } \cdot \frac { 1 } { 3 } = \frac { 4 } { 2 7 } \pi$
知識點:第七章 幾何
對某農村家庭的調查顯示,電冰箱擁有率為49%,電視機擁有率為85%,洗衣機擁有率為44%,至少有兩種電器的占63%,三種電器齊全的占25%,則一種電器都沒有的占比為( )。
- A20%
- B15%
- C10%
- D25%
- E30%
● 正確答案:C
收藏本題 糾錯
答案解析:
設A為擁有電冰箱的家庭,B為擁有電視機的家庭,C為擁有洗衣機的家庭,x為只擁有電冰箱的家庭,y為只擁有電視機的家庭,z為只擁有洗衣機的家庭,根據題意知ABC=0.25,,AB+AC+BC=63%-25%=38%。如圖所示,
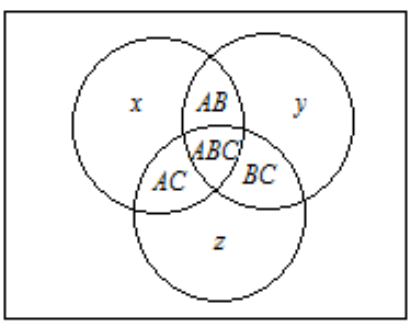
有:$\left\lbrace\begin{array}{l} { x + A B + A C + A B C = 0 . 4 9 } \\ { y + A B + B C + A B C = 0 . 8 5 } \\ { z + B C + A C + A B C = 0 . 4 4 } \end{array}\right.$$\Rightarrow x + y + z + 2 ( A B + B C + A C ) + 3 A B C = 1 . 7 8$$\Rightarrow x + y + z = 0 . 2 7$。所以有$x + y + z + A B + B C + A C + A B C = 0 . 9$。那么一種電器都沒有的比例為10%。
知識點:第十章 概率初步
$( x + \frac { 4 } { x } + 4 ) ^ { 3 }$展開式中的常數項為( )。
- A125
- B-124
- C124
- D-160
- E160
● 正確答案:E
收藏本題 糾錯
答案解析:
解析: $\left(x+\frac{4}{x}+4\right)^3$ 展開式中的常數項是: $C_3^1 \cdot C_2^1 \cdot 4 \cdot C_1^1 \cdot 4+C_3^3 \cdot 4^3=96+64=160$ 。
另解: 因為 $\left(x+\frac{4}{x}+4\right)^3=\left(\frac{x^2+4 x+4}{x}\right)^3=\left[\frac{(x+2)^2}{x}\right]^3=\frac{(x+2)^6}{x^3}$, 所以展開式中的常數項是: $C_6^3 \cdot 2^3=160$ 。
知識點:二項式定理
如圖所示,ABCD頂點的坐標依次為A(-2,2),B(-1,5),C(4,3),D(2,1)則四邊形ABCD的面積等于( )。
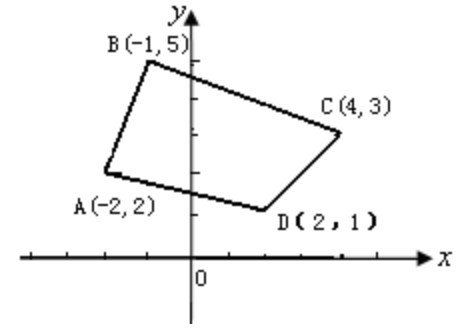
- A16.5
- B15
- C13.5
- D12
- E11.5
● 正確答案:C
收藏本題 糾錯
答案解析:
如圖所示: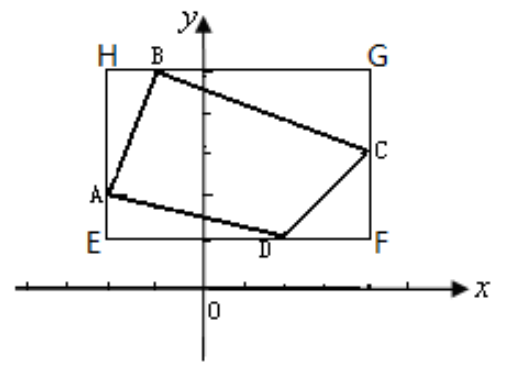
$S _ { A B C D } = S _ { E F G H } - S _ { \Delta A H B } - S _ { \triangle B G C } - S _ { \Delta C F D }- S _ { \Delta D E A }$$= 6 \times 4 - \frac { 1 } { 2 } \times 1 \times 3 - \frac { 1 } { 2 } \times 5 \times 2 - \frac { 1 } { 2 } \times 2 \times 2$$- \frac { 1 } { 2 } \times 1 \times 4 = 1 3 . 5$
知識點:第八章 解析幾何
已知兩圓$C _ { 1 } : x ^ { 2 } + y ^ { 2 } = 1 , \quad C _ { 2 } : ( x - 2 ) ^ { 2 } + ( y - 2 ) ^ { 2 } = 5$,則經過點P(0,1)且被兩圓截得弦長相等的直線方程是( )。
- Ax+y+1=0
- Bx+y-1=0
- Cx+y+1=0或x=1
- Dx+y-1=0或x=1
- Ex+y-1=0或x=0
● 正確答案:E
收藏本題 糾錯
答案解析:
解析: (1) 當直線斜率不存在時, 直線的方程為 $x=0$ 。圓 $C_1$ 所截的弦長為其直徑, 即 $l_1=2$; 圓 $C_2$ 的圓心 $(2,2)$ 到 $x=0$ 的距離為 $d=2$, 所截的弦長為 $l_2=2 \sqrt{r^2-d^2}=2$ 。符合題意要求。
(2) 當直線斜率存在時, 設直線的方程為: $y=k x+1$ 。圓 $C_1$ 的圓心 ( 0,0$)$ 到直線的
距離為 $d_1=\frac{|1|}{\sqrt{1+k^2}}$, 圓 $C_2$ 的圓心 $(2,2)$ 到直線的距離為 $d_2=\frac{|2 k-1|}{\sqrt{1+k^2}}$; 根據題意, 有:$2 \sqrt{1-\frac{1}{1+k^2}}=2 \sqrt{5-\frac{(2 k-1)^2}{1+k^2}}$, 解得 $k=-1$, 所以直線方程為 $y=-x+1$ 。 綜上所述, 直線方程為 $x+y-1=0$ 或 $x=0$ 。
知識點:第八章 解析幾何
甲、乙、丙三人完成某件工作,甲單獨完成工作所用的時間是乙、丙兩人合作所需時間的5 倍,乙單獨完成工作所用的時間與甲、丙兩人合作所需時間相等,則丙單獨完成工作所需時間是甲、乙兩人合作所需時間的( )倍。
- A4
- B3.5
- C3
- D2.5
- E2
● 正確答案:E
收藏本題 糾錯
答案解析:
設甲、乙、丙單獨完成工作所需的時間分別為x、y、z,丙單獨完成工作所需的時間是甲、乙合作所需時間的k倍,工程量為1,則有
$\left\lbrace\begin{array}{l} { \frac { 1 } { y } + \frac { 1 } { z }= \frac { 5 } { x } \ } \\ {\frac { 1 } { x }+\frac { 1 } { z } = \frac { 1 } { y } } \\ { \frac { 1 } { x } + \frac { 1 } { y } = \frac { k } { z } } \end{array}\right.$
令
$\frac { 1 } { x } = a , \frac { 1 } { y } = b , \frac { 1 } { z } = c$,
則有
$\left\lbrace\begin{array}{l} { b + c = 5 a } \\ { a + c = b } \\ { a + b = kc } \end{array}\right.\Rightarrow \left\lbrace\begin{array}{l} { b = 3 a } \\ { c = 2 a } \\ { a + 3 a = k \cdot 2 a } \end{array}\right. \Rightarrow k=2$
知識點:工程問題
已知三個不同的質數 a,b, c 滿足$a b ^ { b } c + a = 2 0 0 0$,則a+b+ c =( )
- A39
- B40
- C41
- D42
- E43
● 正確答案:D
收藏本題 糾錯
答案解析:
解析:由$a b ^ { b } c + a = 2 0 0 0$,可知$a ( b ^ { b } c + 1 ) = 2 ^ { 4 } \times 5 ^ { 3 }$,可知a=2或a=5。若a=2,則$b ^ { b } c = 9 9 9 = 3 ^ { 3 } \times 3 7$,因此b=3,c=37,若a=5,則$b ^ { b } c = 3 9 9 = 3 \times 7 \times 1 9$不符合題意。
知識點:實數及其運算
在數列$\lbrace a _ { n } \rbrace$中,$a _ { 1 } = 1 , a _ { 2 } = 3$,則$\frac { a _ { n + 2 } } { a _ { n } } = 2 ( n = 1 , 2 , 3 \cdots )$,則$S _ { 1 1 }$=( )
- A156
- B128
- C116
- D96
- E86
● 正確答案:A
收藏本題 糾錯
答案解析:
此數列為 1,3,2,6,4,12,8,24,16,48,32
$S _ { 1 1 }$=(1+2+4+8+16+32)+(3+6+12+24+48)
=$ \frac { 1 - 2 ^ { 6 } } { 1 - 2 } + \frac { 3 ( 1 - 2 ^ { 5 } ) } { 1 - 2 }$
=63+93
=156
知識點:第五章 數列
如圖所示,正方形ABCD的面積為$1$,以A為圓心作$\frac{1}{4}$的扇形弧BD,以AB為直徑作半圓弧AB,M是AD上一點,以DM為直徑作半圓弧DM與半圓弧AB外相切,則圖中陰影部分的面積為( )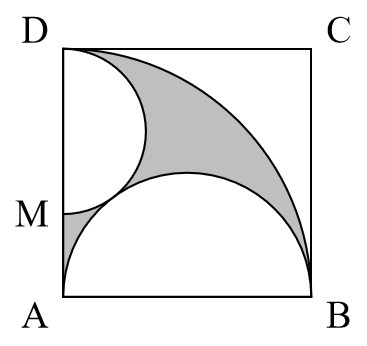
- A$\frac{5\pi}{16}$
- B$\frac{5\pi}{32}$
- C$\frac{\pi}{16}$
- D$\frac{5\pi}{64}$
- E$\frac{5\pi}{72}$
● 正確答案:E
收藏本題 糾錯
答案解析:

知識點:圓和扇形面積
己知$0<k<4$,直線$ l _ { 1 } : k x - 2 y - 2 k + 8 = 0 $和直線$ l _ { 2 } : 2 x + k ^ { 2 } y - 4 k ^ { 2 } - 4 = 0 $與兩坐標軸圍成一個四邊形,則使得這個四邊形面積最小的$k$值為( )
- A$ \frac{1}{4}$
- B$ \frac{1}{8}$
- C$ \frac{1}{6}$
- D$ \frac{1}{2}$
- E$ \frac{1}{3}$
● 正確答案:B
收藏本題 糾錯
答案解析:
直線$ l _ { 1 }, l _ { 2 }$恒過定點$P(2,4)$,直線$l _ { 1 }$在$y$軸上的截距為$4-k$,直線$ l _ { 2 }$在$x$軸上的截距為$ 2 k ^ { 2 } + 2 $,因為0<k<4
$ S = \frac { 1 } { 2 } \times 4 \times ( 2 k ^ { 2 } + 2 ) + \frac { 2 \times ( 4 - k ) } { 2 } = 4 k ^ { 2 } - k + 8 $
所以當$ k=\frac{1}{8}$時,四邊形面積最小,選B
知識點:直線位置關系
網球比賽的規則是$5$局$3$勝制,甲、乙兩人每局比賽獲勝的概率分別為$\frac { 2 } { 3 }$和$\frac { 1 } { 3 }$,前$2$局中乙以$2:0$領先,則最后乙獲勝的概率為( ).
- A$\frac { 19 } { 27 }$
- B$\frac { 20 } { 27 }$
- C$\frac { 7 } { 9 }$
- D$\frac { 22 } { 27 }$
- E$\frac { 8 } { 9 }$
● 正確答案:A
收藏本題 糾錯
答案解析:
乙只需要再贏得一局就獲勝,則有三種情況,分別在第三、四、五局獲勝,所以乙獲勝的概率是$P = \frac { 1 } { 3 } + \frac { 2 } { 3 } \times \frac { 1 } { 3 } + \frac { 2 } { 3 } \times \frac { 2 } { 3 } \times \frac { 1 } { 3 } = \frac { 1 9 } { 2 7 }$.
知識點:古典概型
甲、乙、丙三名射箭運動員在某次測試中各射擊20次,三人的測試成績如下表:
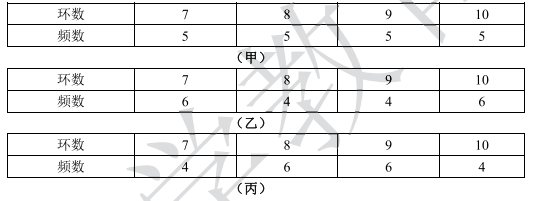
$S_{1},S_{2},S_{3}$分別表示甲、乙、丙三名運動員這次測試成績的方差,則有( ).
- A$S_{3}>S_{1}>S_{2}$
- B$S_{2}>S_{1}>S_{3}$
- C$S_{1}>S_{2}>S_{3}$
- D$S_{1}>S_{3}>S_{2}$
- E$S_{2}>S_{3}>S_{1}$
● 正確答案:B
收藏本題 糾錯
答案解析:
因為甲、乙、丙三名運動員測試成績的平均值都是8.5,方差表示數據的波動程度, 平均數相同,波動大方差大,三組數據乙的波動最大,甲次之,丙最小,所以選B.
知識點:平均值
某股票周二開盤時比周一開盤時價格下跌 20%,周三比周二下跌 30%,到周四開盤時該股票又上升到周一的開盤價,則從周三到周四該股票上升的百分比約為( )。
- A50%
- B60.67%
- C72.33%
- D78.57%
- E80%
● 正確答案:D
收藏本題 糾錯
答案解析:
答案:D 解析:設周一開盤價為 $a$,則根據題意,有: $a \rightarrow 0 . 8 a \rightarrow 0 . 7 \times 0 . 8 a \rightarrow a $,從而$\frac { a - 0 . 7 \times 0 . 8 a } { 0 . 7 \times 0 . 8 a } = 7 8 . 5 7 \%$。
知識點:比例問題
已知方程$( x ^ { 2 } - 2 x + p ) ( x ^ { 2 } - 2 x + q ) = 0 \quad ( p \neq q ) $的4個實根構成一個首項為$\frac{1}{4}$的等差數列,則$\left |p-q \right |=$( )。
- A2
- B1
- C$\frac{3}{8}$
- D$\frac{3}{4}$
- E$\frac{1}{2}$
● 正確答案:E
收藏本題 糾錯
答案解析:
解析:設4個根為$x _ { 1 } = \frac { 1 } { 4 } , x _ { 2 } = \frac { 1 } { 4 } + d , x _ { 3 } = \frac { 1 } { 4 } + 2 d , x _ { 4 } = \frac { 1 } { 4 } + 3 d$
由于$ \frac { 1 } { 4 } + \frac { 1 } { 4 } + 3 d = \frac { 1 } { 4 } + d + \frac { 1 } { 4 } + 2 d $,即$ x _ { 1 } + x _ { 4 } = x _ { 2 } + x _ { 3 } = 2$
$\frac { 1 } { 2 } + 3 d = 2 , \quad d = \frac { 1 } { 2 }$
$x _ { 1 } x _ { 4 } = p = \frac { 7 } { 1 6 }; x _ { 2 } x _ { 3 } = q= \frac { 1 5 } { 1 6 }$
則$|\frac{7}{16}-\frac{15}{16}|=\frac{1}{2}$
知識點:等差數列
某國際會議參加人員中,有85%的人懂英文,49%的人懂法文,44%的人懂中文,三種語言都懂的有30%,三種語言都不懂的有10%,則懂兩種或兩種以上語言的人數為( )。
- A40%
- B58%
- C50%
- D54%
- E55%
● 正確答案:B
收藏本題 糾錯
答案解析:
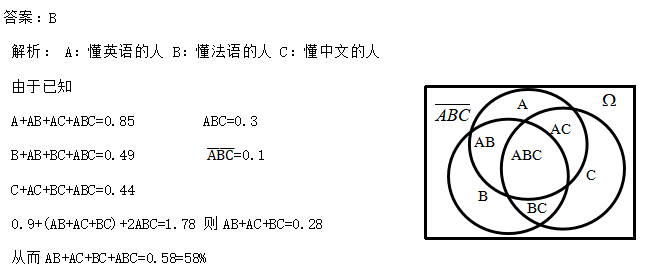
知識點:方氏圖和容斥定理
已知$\frac { 1 } { a } < \frac { 1 } { b } < 0$,則下列不等式中成立的是( )
$( 1 ) \quad a + b < a b $
$( 2 ) \quad | a | > | b | \quad $
$( 3 )a < b $
$( 4 )\frac { b } { a } + \frac { a } { b } > 2$
- A(1)(4)
- B(1)(3)
- C(2)(3)
- D(2)(4)
- E(4)
● 正確答案:A
收藏本題 糾錯
答案解析:
用代入法 取 a=1, b=-2 ; a=-2, b=-3可知⑴和⑷成立。
知識點:不等式
$\lbrace a _ { n } \rbrace 為等比數列,a _ { 2 } = 2 , a _ { 5 } = \frac { 1 } { 4 }$ 則 $ a _ { 1 } a _ { 2 } + a _ { 2 } a _ { 3 } + \cdots + a _ { n } a _ { n + 1 } =( )$
- A$\frac { 3 2 } { 3 } ( 1 - 4 ^ { n } )$
- B$\frac { 3 2 } { 3 } ( 4 ^ { n }-1 )$
- C$\frac { 3 2 } { 3 } ( 4 ^ { -n }-1 )$
- D$\frac { 3 2 } { 3 } ( 1- 4 ^ { -n } )$
- E$\frac { 3 2 } { 3 } ( 4 ^ { -n }+1 )$
● 正確答案:D
收藏本題 糾錯
答案解析:

知識點:等比數列
已知$a$,$b$,$c$為實數,且多項式$x^3+ax^2+bx+c$被除$x^2-3x+2$,其余式為$x+2$,則$4a+2b+c$( )
- A8
- B4
- C0
- D-4
- E-8
● 正確答案:D
收藏本題 糾錯
答案解析:
解析:根據題意設$x^3+ax^2+bx+c=(x^2-3x+2)\cdot q(x)+x+2$,即$x^3+ax^2+bx+c=(x-1)\cdot (x-2)\cdot q(x)+x+2$。
令$x=1$,則有$1+a+b+c=3$ (1);
令$x=2$,則有$8+4a+2b+c=4$ (2);
聯立(1)(2)解得
$\left\{\begin{matrix}a=\frac{c-8}{2}\\ b=\frac{-3c+12}{2}\end{matrix}\right.$
那么$4a+2b+c=4\cdot \frac{c-8}{2}+2\cdot \frac{-3c+12}{2}+c=-4$。
知識點:余式定理與因式定理
甲容器中有純酒精 11 升,乙容器中有水 15 升,第一次將甲容器中的一部分純酒精倒入乙容器,使酒精與水混合;第二次將乙容器中的一部分混合液倒入甲容器,這樣甲容器的溶液濃度為 62.5%,乙容器的溶液濃度為 25%,則從乙容器倒入甲容器的混合液有( )升。
- A8
- B7
- C6
- D5
- E4
● 正確答案:C
收藏本題 糾錯
答案解析:
設甲倒出 $x$ 升, 乙倒出 $y$ 升, 那么根據題意有 $\left\{\begin{array}{c}\frac{x}{15+x}=0.25 \\ \frac{11-x+0.25 y}{11-x+y}=0.625\end{array}\right.$, 解得$\left\{\begin{array}{l}x=5 \\y=6\end{array}\right.$。
知識點:溶液問題
條件充分性判斷
有英語、數學、邏輯共5本不同的書,若將其隨機地并排擺放到書架的同一層上,則同一科目的書都不相鄰的概率是$\frac{2}{5}$
(1)其中英語書2本,數學書2本,邏輯書1本.
(2)其中英語書3本,數學書1本,邏輯書1本.
- A條件(1)充分,但條件(2)不充分
- B條件(2)充分,但條件(1)不充分
- C條件(1)和(2)單獨都不充分,但條件(1)和條件(2)聯合起來充分
- D條件(1)充分,條件(2)也充分
- E條件(1)和(2)單獨都不充分,條件(1)和條件(2)聯合起來也不充分
● 正確答案:A
收藏本題 糾錯
答案解析:
(1)第一類:先排英語書,有2種,邏輯書排英語書中間,這樣有4個空位可以 插入,有$C _ { 4 } ^ { 2 } \times 2 ! $種,故有24種;第二類,先排英語書,有2種,邏輯書不排英語書中間, 英語書中間只能排數學書,剩下兩個可以排在一起或排在兩端,有$C _ { 2 } ^ { 1 } \times 2 \times ( 2 + C _ { 2 } ^ { 1 } \times 2 ) = 2 4 $種,故概率為$\frac { 2 4 + 2 4 } { 5 ! } = \frac { 2 } { 5 } $(2)共有$2 ! \times 3 ! = 1 2$ 種,概率為 $\frac { 1 2 } { 5 ! } = \frac { 1 } { 1 0 } $。
知識點:古典概型
已知 $a 、 b 、 c$ 三種水果的價格分別為 $x$ 元/千克、 $y$ 元/千克、 $z$ 元/千克, 則三種水果的平均價格不低于 10 元/千克。
(1)三種水果的價格最低為 8 元/千克
(2)購買 $a 、 b 、 c$ 三種水果的重量分別為 1 千克、1 千克、2 千克共用了 46 元
- A條件1充分,但條件2不充分;
- B條件2充分,但條件1不充分;
- C條件1和2單獨都不充分,但條件1和條件2聯合起來充分;
- D條件1充分,條件2也充分;
- E條件1和2單獨都不充分,條件1和條件2聯合起來也不充分;
● 正確答案:C
收藏本題 糾錯
答案解析:
解析: 條件(1)和條件(2)單獨顯然不充分。聯合起來, 有:
$x+y+2 z=46$, 若 $x=y=8$, 則 $z=15$; 那么 $\frac{x+y+z}{3}>10$ 。所以條件(1)和條件(2)聯合起來充分。
知識點:實數及其運算
$N=48$
(1) 6 個人坐兩排, 每排有 3 個座位, 其中甲、乙兩人必須相鄰, 且丙不能坐在兩端, 有 $N$ 種不同的坐法
(2) 6 個人坐兩排, 每排有 3 個座位, 其中甲、乙兩人必須在同排, 且與丙不在同一排, 有 2 N 種不同的坐法
- A條件1充分,但條件2不充分;
- B條件2充分,但條件1不充分;
- C條件1和2單獨都不充分,但條件1和條件2聯合起來充分;
- D條件1充分,條件2也充分;
- E條件1和2單獨都不充分,條件1和條件2聯合起來也不充分;
● 正確答案:A
收藏本題 糾錯
答案解析:
解析: 由條件 (1), 在每排的 3 個座位中, 兩個座位相鄰的有 4 種情況, 從 4 中選出 1 個, 有 $C_4^1$ 種; 甲乙兩人相鄰有 $2 !$ 種; 又丙不能坐在兩端, 所以丙只有 1 種做法; 乘下的 3 個人沒有要求, 所以有 $3 !$ 種。那么 $N=C_4^1 \cdot 2 ! \cdot 1 \cdot 3 !=48$, 所以條件 (1) 充分。
由條件 (2), $2 N=C_2^1 \cdot C_3^2 \cdot 2 ! \cdot C_3^1 \cdot 3 !=216$, 所以 $N=108$ 。即條件 (2) 不充分。
知識點:排列組合
數列$\lbrace \frac { 1 } { a _ { n } \cdot a _ { n + 1 } } \rbrace$的前 n 項和為$\frac { n } { a _ { 1 } \cdot a _ { n + 1 } }$
(1)數列$\lbrace a _ { n } \rbrace $為等差數列
(2)數列$\lbrace a _ { n } \rbrace $為等比數列
- A條件1充分,但條件2不充分;
- B條件2充分,但條件1不充分;
- C條件1和2單獨都不充分,但條件1和條件2聯合起來充分;
- D條件1充分,條件2也充分;
- E條件1和2單獨都不充分,條件1和條件2聯合起來也不充分;
● 正確答案:A
收藏本題 糾錯
答案解析:
由條件( 1 ),設公差為d ,那么數列$\lbrace \frac { 1 } { a _ { n } \cdot a _ { n + 1 } } \rbrace$的前 n 項和為$S_n=\frac{1}{a_1 a_2}+\frac{1}{a_2 a_3}+\frac{1}{a_3 a_4}+\cdots+\frac{1}{a_n a_{n+1}}=\frac{1}npz7bfj\left(\frac{1}{a_1}-\frac{1}{a_2}+\frac{1}{a_2}-\frac{1}{a_3}+\cdots+\frac{1}{a_n}-\frac{1}{a_{n+1}}\right)$$= \frac { 1 } { d } ( \frac { 1 } { a _ { 1 } } - \frac { 1 } { a _ { n + 1 } } ) = \frac { n } { a _ { 1 } \cdot a _ { n + 1 } }$。所以條件(1)充分,條件(2)不充分
知識點:第五章 數列
不等式$\left|x+\log _3 x\right|<|x|+\left|\log _3 x\right|$
(1) $x>0$
(2) $x<1$
- A條件1充分,但條件2不充分;
- B條件2充分,但條件1不充分;
- C條件1和2單獨都不充分,但條件1和條件2聯合起來充分;
- D條件1充分,條件2也充分;
- E條件1和2單獨都不充分,條件1和條件2聯合起來也不充分;
● 正確答案:C
收藏本題 糾錯
答案解析:
取 $x=1, x=0$, 則知條件(1)和條件(2)都不充分。 聯合條件(1)和條件(2)
$|a+b|<|a|+|b| \Leftrightarrow a b<0$,即 $ x \log _3 x<0$,即 $0<x<1$
知識點:絕對值
數據$S_1: a, b, c$與數據$S_2$的標準差相等.
(1)數據$S_2: a-2, b-2, c-2$
(2)數據$S_2: 0, b-c, b-a$
- A條件1充分,但條件2不充分;
- B條件2充分,但條件1不充分;
- C條件1和2單獨都不充分,但條件1和條件2聯合起來充分;
- D條件1充分,條件2也充分;
- E條件1和2單獨都不充分,條件1和條件2聯合起來也不充分;
● 正確答案:D
收藏本題 糾錯
答案解析:

知識點:方差、圖表
某公司有10個股東,則持股最多的股東所持股份占總股份的最大百分比不超過25%。
⑴ 他們中任意6個股東所持股份的和不都少于總股份的50%。
⑵ 他們中任意3個股東所持股份的和都不少于總股份的25%。
- A條件1充分,但條件2不充分;
- B條件2充分,但條件1不充分;
- C條件1和2單獨都不充分,但條件1和條件2聯合起來充分;
- D條件1充分,條件2也充分;
- E條件1和2單獨都不充分,條件1和條件2聯合起來也不充分;
● 正確答案:D
收藏本題 糾錯
答案解析:
知識點:比例問題
在直角坐標系中,直線$y=kx$與
$y=\left\lbrace\begin{array}{l} { 2x+4,x
(1)$0<k<1$
(2)$\frac{1}{2}<k<2$
- A條件1充分,但條件2不充分;
- B條件2充分,但條件1不充分;
- C條件1和2單獨都不充分,但條件1和條件2聯合起來充分;
- D條件1充分,條件2也充分;
- E條件1和2單獨都不充分,條件1和條件2聯合起來也不充分;
● 正確答案:E
收藏本題 糾錯
答案解析:

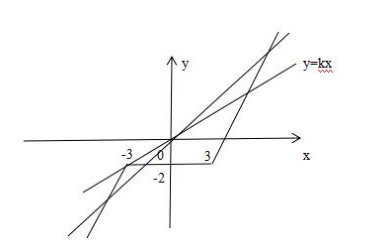
知識點:直線位置關系
開運動會時,某班28名同學參加比賽,有15人參加游泳比賽,有8人參加田徑比賽,有14人參加球類比賽,同時沒有參加三項比賽的人。則只參加田徑比賽有2人。
(1)參加游泳和田徑比賽的有3人
(2)參加游泳和球類比賽的有3人
- A條件1充分,但條件2不充分;
- B條件2充分,但條件1不充分;
- C條件1和2單獨都不充分,但條件1和條件2聯合起來充分;
- D條件1充分,條件2也充分;
- E條件1和2單獨都不充分,條件1和條件2聯合起來也不充分;
● 正確答案:B
收藏本題 糾錯
答案解析:
解析:由條件(1),設參加球類和田徑比賽的有$x$人,參加游泳和球類比賽的有$y$人,如圖所示:
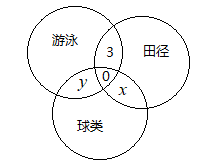
那么有$15+14-x-y+5=28\Rightarrow x+y=6$,不能得出只參加田徑比賽的人數。所以條件(1)不充分。
由條件(2),參加球類和田徑比賽的有$x$人,設參加游泳和田徑比賽的有$y$人,如圖所示:
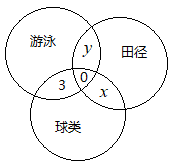
那么有$15+11+8-x-y=28\Rightarrow x+y=6$,所以只參加田徑比賽的人數為$8-(x+y)=2$人。所以條件(2)充分。
知識點:集合
$x^2+y^2+z^2-xy-yz-zx$的最小值為75。
(1)$x-y=10$
(2)$y-z=10$
- A條件1充分,但條件2不充分;
- B條件2充分,但條件1不充分;
- C條件1和2單獨都不充分,但條件1和條件2聯合起來充分;
- D條件1充分,條件2也充分;
- E條件1和2單獨都不充分,條件1和條件2聯合起來也不充分;
● 正確答案:D
收藏本題 糾錯
答案解析:
解析:
由條件(1),令$y-z=a$,則$x-z=a+10$。那么原式$=\frac{1}{2}\left [ (x-y)^2+(y-z)^2+(z-x)^2 \right ]=\frac{1}{2}(100+a^2+a^2+20a+100)=a^2+10a+100=(a+5)^2+75\geq 75$。
所以條件(1)充分。同理條件(2)也充分。
知識點:代數式的計算
- 十六進制
- 十進制
- 八進制
- 二進制
- 角度制
- 弧度制
- 上檔功能
- 雙曲函數
開始做題