2024年6月第4周每日一練題目匯
- 問題求解
- 條件充分性判斷
- 邏輯推理
打印試卷
問題求解
已知數列$ \lbrace a _ { n } \rbrace , \quad a _ { 1 } = 3 , \quad a _ { 2 } = 6 , \quad a _ { n + 2 } = a _ { n + 1 } - a _ { n } , $則$a _ { 2 0 1 0 } $= ( )
- A-6
- B-5
- C-3
- D0
- E3
● 正確答案:C
收藏本題 糾錯
答案解析:
解析:$a _ { 1 } = 3 , a _ { 2 } = 6 , a _ { 3 } = 3 , a _ { 4 } = - 3 , a _ { 5 } = - 6 , a _ { 6 } = -3 , a _ { 7 } = 3 , a _ { 8 } = 6 , $所以6個一循環,和為0,所以 2010=6×335 ,所以$a _ { 2 0 1 0 } = a _ { 6 } = - 3 $
知識點:等差數列
設數列$\lbrace a _ { n } \rbrace$的前n項和$S _ { n } = n ^ { 2 } + n$,則$\frac { 1 } { a _ { 1 } a _ { 2 } } + \frac { 1 } { a _ { 2 } a _ { 3 } } + \cdots + \frac { 1 } { a _ { 9 } a _ { 1 0 } }$=( )
- A$\frac { 3 } { 4 0 }$
- B$\frac { 7 } { 4 0 }$
- C$\frac { 9 } { 4 0 }$
- D$\frac { 11 } { 4 0 }$
- E$\frac { 13 } { 4 0 }$
● 正確答案:C
收藏本題 糾錯
答案解析:
由數列前n 項和與數列通項之間的關系可知,該數列為等差數列,通項公式為$?a _ { n } = 2 n$,由分數裂項的方法可知結果為$\frac { 9 } { 4 0 }$。
知識點:第五章 數列
在數列$\lbrace a _ { n } \rbrace$中,$a _ { 1 } = 1 , a _ { 2 } = 3$,則$\frac { a _ { n + 2 } } { a _ { n } } = 2 ( n = 1 , 2 , 3 \cdots )$,則$S _ { 1 1 }$=( )
- A156
- B128
- C116
- D96
- E86
● 正確答案:A
收藏本題 糾錯
答案解析:
此數列為 1,3,2,6,4,12,8,24,16,48,32
$S _ { 1 1 }$=(1+2+4+8+16+32)+(3+6+12+24+48)
=$ \frac { 1 - 2 ^ { 6 } } { 1 - 2 } + \frac { 3 ( 1 - 2 ^ { 5 } ) } { 1 - 2 }$
=63+93
=156
知識點:第五章 數列
若等差數列 $\left\{a_n\right\}$ 與等比數列 $\left\{b_n\right\}$ 滿足 $a_1=b_1=-1, a_4=b_4=8$, 則 $\frac{a_2}{b_2}$ 的值為 ( )。
- A5
- B4
- C3
- D2
- E1
● 正確答案:E
收藏本題 糾錯
答案解析:
由于 $a_4=a_1+3 d=-1+3 d=8 \Rightarrow d=3$, 所以 $a_2=a_1+d=-1+3=2$; 又 $b_4=b_1 \cdot q^3=-1 \cdot q^3=8 \Rightarrow q=-2$, 所以 $b_2=b_1 \cdot q=-1 \cdot(-2)=2$, 那么 $\frac{a_2}{b_2}=1$ 。
知識點:第五章 數列
等差數列$\lbrace a _ { n } \rbrace $的前n項和為$S _ { n } $,且$a _ { m + 1 } + a _ { m - 1 } - a _ { m } ^ { 2 } = 0 , \quad S _ { 2 m - 1 } = 3 8 . $,則m=( )
- A38
- B20
- C10
- D9
- E5
● 正確答案:C
收藏本題 糾錯
答案解析:
因為$\lbrace a _ { n } \rbrace $是等差數列,所以$a _ { m + 1 } + a _ { m - 1 } = 2 a _ { m } $,由$a _ { m + 1 } + a _ { m - 1 } - a _ { m } ^ { 2 } = 0 $得$a _ { m } = 2$,又$S _ { 2 m - 1 } = ( 2 m - 1 ) a _ { m } = 2 ( 2 m - 1 ) = 3 8 \rightarrow m = 1 0 $
知識點:等差數列
已知數列$\lbrace a _ { n } \rbrace$的通項公式為$a _ { n } = 3 ^ { n } + 2 ^ { n } + 2 n - 1 $,則前5項和為( ).
- A225
- B350
- C320
- D450
- E500
● 正確答案:D
收藏本題 糾錯
答案解析:
$S _ { 5 } = \frac { 3 ( 1 - 3 ^ { 5 } ) } { 1 - 3 } + \frac { 2 ( 1 - 2 ^ { 5 } ) } { 1 - 2 } + 5 \times 5 = 4 5 0$.
知識點:等差數列
若$6,a,c$成等差數列,$ 3 6 , a ^ { 2 } , - c ^ { 2 } $也成等差數列,則$c$= ( )
- A-6
- B-5
- C2
- D-6或2
- E$ \pm 5 $
● 正確答案:D
收藏本題 糾錯
答案解析:
依題可得方程組$ \left\lbrace\begin{array}{l} { 2 a = 6 + c } \\ { 2 a ^ { 2 } = 3 6 - c ^ { 2 } } \end{array}\right. $,解得$c=-6,2$選D
知識點:等差數列
方程$x\left | x \right |-3\left | x \right |+2=0$的不同根共( )個.
- A1
- B2
- C3
- D4
- E0
● 正確答案:C
收藏本題 糾錯
答案解析:
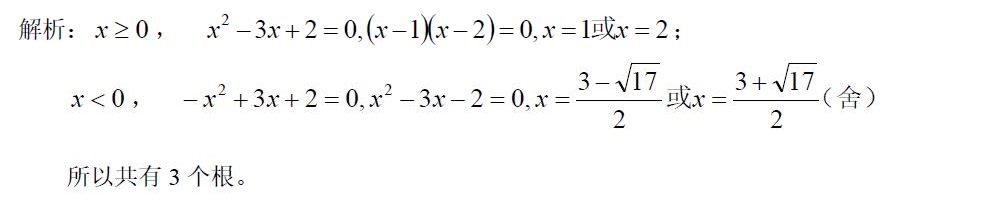
知識點:方程實根分布問題
已知$\lbrace a _ { n } \rbrace$為等差數列,若$a _ { 2 }$ ,$a _ { 3 }$ ,$a _ { 7 }$成等比數列,且 $2 a _ { 1 } + a _ { 2 } = 1$ ,則 $a _ { 5 }$ 的值為( )
- A$- \frac { 7 } { 3 }$
- B$- \frac { 8 } { 3 }$
- C-3
- D$- \frac { 10 } { 3 }$或$ \frac { 1 } { 3 }$
- E$- \frac { 11 } { 3 }$
● 正確答案:D
收藏本題 糾錯
答案解析:
根據題意,有$\left\lbrace\begin{array}{l} { ( a _ { 1 } + 2 d ) ^ { 2 } = ( a _ { 1 } + d ) ( a _ { 1 } + 6 d ) } \\ { 3 a _ { 1 } + d = 1 } \end{array}\right.$$\Rightarrow \left\lbrace\begin{array}{l} { a _ { 1 } = \frac { 2 } { 3 } } \\ { d = - 1 } \end{array}\right.$,或$\left\lbrace\begin{array}{l} { a _ { 1 } = \frac { 1 } { 3 } } \\ { d = 0 } \end{array}\right.$,那么$a _ { 5 } = a _ { 1 } + 4 d = - \frac { 1 0 } { 3 }$或$a _ { 5 } = \frac { 1 } { 3 }$
知識點:第五章 數列
條件充分性判斷
不等式 $|x+1|+|x-1| \leq a$ 在實數集上的解集非空。
(1) $\sqrt{a-2}+\sqrt{2-a}$ 有意義
(2) $|a-1|<2$
- A條件1充分,但條件2不充分;
- B條件2充分,但條件1不充分;
- C條件1和2單獨都不充分,但條件1和條件2聯合起來充分;
- D條件1充分,條件2也充分;
- E條件1和2單獨都不充分,條件1和條件2聯合起來也不充分;
● 正確答案:A
收藏本題 糾錯
答案解析:
解析: 令 $f(x)=|x+1|+|x-1|$, 則 $f(x)=\left\{\begin{array}{c}-2 x, x \leq-1 \\ 2,-1<x<1 \\ 2 x, x \geq 1\end{array}\right.$。
所以不等式 $|x+1|+|x-1| \leq a$ 在實數集上的解集非空, 則 $a$ 的取值范圍為: $a \geq 2$ 。
由條件 (1), 得 $\left\{\begin{array}{l}a-2 \geq 0 \\ 2-a \leq 0\end{array} \Rightarrow a=2\right.$ 。所以條件 (1) 充分。
由條件 (2), 得 $-2<a-1<2 \Rightarrow-1<a<3$ 。所以條件 (2) 不充分。
知識點:其他不等式
數列$\lbrace \frac { 1 } { a _ { n } \cdot a _ { n + 1 } } \rbrace$的前 n 項和為$\frac { n } { a _ { 1 } \cdot a _ { n + 1 } }$
(1)數列$\lbrace a _ { n } \rbrace $為等差數列
(2)數列$\lbrace a _ { n } \rbrace $為等比數列
- A條件1充分,但條件2不充分;
- B條件2充分,但條件1不充分;
- C條件1和2單獨都不充分,但條件1和條件2聯合起來充分;
- D條件1充分,條件2也充分;
- E條件1和2單獨都不充分,條件1和條件2聯合起來也不充分;
● 正確答案:A
收藏本題 糾錯
答案解析:
由條件( 1 ),設公差為d ,那么數列$\lbrace \frac { 1 } { a _ { n } \cdot a _ { n + 1 } } \rbrace$的前 n 項和為$S_n=\frac{1}{a_1 a_2}+\frac{1}{a_2 a_3}+\frac{1}{a_3 a_4}+\cdots+\frac{1}{a_n a_{n+1}}=\frac{1}6w0osse\left(\frac{1}{a_1}-\frac{1}{a_2}+\frac{1}{a_2}-\frac{1}{a_3}+\cdots+\frac{1}{a_n}-\frac{1}{a_{n+1}}\right)$$= \frac { 1 } { d } ( \frac { 1 } { a _ { 1 } } - \frac { 1 } { a _ { n + 1 } } ) = \frac { n } { a _ { 1 } \cdot a _ { n + 1 } }$。所以條件(1)充分,條件(2)不充分
知識點:第五章 數列
若$S_{n}$是等差數列{$a_{n}$}的前n項和,則$S_{n}$≤$S_{10}$ (n=1,23..)
(1) $S_{19}$=0
(2) $a_{1}$>0
- A條件(1)充分,但條件(2)不充分.
- B條件(2)充分,但條件(1)不充分.
- C條件(1)和條件(2)單獨都不充分,但條件(1)和條件(2)聯合起來充分.
- D條件(1)充分,條件(2)也充分.
- E條件(1)和條件(2)單獨都不充分, 條件(1)和條件(2)聯合起來也不充分.
● 正確答案:C
收藏本題 糾錯
答案解析:
解析:條件(1), $S_{19}$=0,所以$S_{n}$拋物線的對稱軸是n=9.5,所以當$S_{9}$=$S_{10}$,離對稱軸最近,但是不知道開口方向,需要條件(2)聯合,$a_{1}$>0, $S_{19}$=0,遞減數列,d<0,開口朝下,有$S_{9}$=$S_{10}$為$S_{n}$的最大值,聯合充分,選C
知識點:等差數列
在等差數列$\lbrace a _ { n } \rbrace$中,其前$n$項和為$S _ { n }$,則$S _ { 2 0 0 8 } = - 2 0 0 8$.
(1)$a _ { 1 } = - 2 0 0 8$.
(2)$\frac { S _ { 1 2 } } { 1 2 } - \frac { S _ { 1 0 } } { 1 0 } = 2$.
- A條件(1)充分,但條件(2)不充分.
- B條件(2)充分,但條件(1)不充分.
- C條件(1)和(2)單獨都不充分,但是條件(1)和(2)聯合起來充分.
- D條件(1)充分,條件(2)也充分.
- E條件(1)和(2)單獨都不充分,聯合起來也不充分.
● 正確答案:C
收藏本題 糾錯
答案解析:
先由(2)得$\frac { S _ { 1 2 } } { 1 2 } - \frac { S _ { 1 0 } } { 1 0 } = \frac{\frac { ( 2 a_{1} + 1 1 d ) \times 1 2 } { 2 }} { 1 2 } -\frac{\frac { ( 2 a_{1} + 9 d ) \times 1 0 } { 2 }} { 1 0 } = 2\Rightarrow d = 2$,則聯合條件可得
$S _ { 2008 }= \frac { 1 } { 2 } ( a_{1} + a_{1} + 2 0 0 7d ) \times 2 0 0 8= \frac { 1 } { 2 } ( - 2 0 0 8 - 2 0 0 8 + 2 0 0 7 \times 2 ) \times 2 0 0 8 = - 2 0 0 8$.
知識點:等差數列
關于$x$的一元四次方程$x ^ { 4 } - 2 x ^ { 2 } + k = 0$有四個相異的實根。
(1)$1<k<2$
(2)$0<k<\frac{1}{2}$
- A條件1充分,但條件2不充分;
- B條件2充分,但條件1不充分;
- C條件1和2單獨都不充分,但條件1和條件2聯合起來充分;
- D條件1充分,條件2也充分;
- E條件1充分,條件2也充分;
● 正確答案:B
收藏本題 糾錯
答案解析:
設$x^{2}=t$,題干等價于方程$t ^ { 2 } - 2 t + k = 0$有兩個不相等的正實根,則有
$\left\lbrace\begin{array}{l} { \Delta = 4 - 4 k > 0 } \\ { t _ { 1 } + t _ { 2 } = 2 > 0 } \\ { t _ { 1 } t _ { 2 } = k > 0 } \end{array}\right.\Rightarrow 0<k<1$.
所以條件(1)不充分,條件(2)充分。
知識點:方程實根分布問題
方程$x^{2}-2mx+m^{2}-4=0$ 有兩個不相等的實根
(1)m>4
(2) m>3
- A條件1充分,但條件2不充分;
- B條件2充分,但條件1不充分;
- C條件1和2單獨都不充分,但條件1和條件2聯合起來充分;
- D條件1充分,條件2也充分;
- E條件1和2單獨都不充分,條件1和條件2聯合起來也不充分;
● 正確答案:D
收藏本題 糾錯
答案解析:
$\Delta =4m^{2}-4(m^{2}-4)=4m^{2}-4m^{2}+16>0$
所以無論m取何值,此方程永遠有兩個不等實根
知識點:方程實根分布問題
邏輯推理
分手不僅令人心理痛苦,還可能造成身體疼痛。美國研究人員征募40名志愿者,他們在過去半年中被迫與配偶分手,至今依然相當介意遭人拒絕。研究人員借助功能性磁共振成像技術觀察志愿者的大腦活動,結果發現他們對分手等社會拒絕產生反應的大腦部位與對軀體疼痛反應的部位重合,因此分手這類社會拒絕行為會引起他們軀體疼痛。上述推論隱含的假設是什么?
- A個體對于疼痛的感受與社會應激事件有密切關系。
- B功能性磁共振技術是目前進行大腦定位的常用方法。
- C個體情緒等心理過程的改變能影響其生理反應。
- D生理與心理反應可以通過大腦產生關聯。
- E生理上的痛苦總是要通過心理活動來體現。
● 正確答案:D
收藏本題 糾錯
答案解析:
【考點:假設】解析:A選項過度假設,社會應激事件范圍較大,而題干只需要保證分手與身體疼痛相關即可。B選項與題干論證無關。C、E選項是指心里反應直接影響生理行為,但題干強調的是心理行為通過大腦對于生理行為的反應。D選項需要假設,保證了題干的大腦部位和身體疼痛之間存在論證關系,如果不能通過大腦關聯產生反應,那么題干的心理行為和生理之間的關系就不一定存在。
知識點:假設
當兩棲動物在幾百萬年前首次出現在地球上時,穿透地球大氣層的紫外線輻射量比現在大得多。因此,現在兩棲動物數量劇減不會是最近穿透地球大氣層的紫外線輻射增加的結果。
以上論述基于下列哪項假設?
- A現代兩棲動物的卵并不比最初兩棲動物的卵顯著地更易受紫外線輻射的傷害。
- B現代兩棲動物的棲息地不大可能像早期兩棲動物的棲息地那樣能夠遮蔽紫外線。
- C現在兩棲動物不能像早期兩棲動物那樣容易地適應輻射程度的改變。
- D兩棲動物的皮膚通常比其他動物的皮膚對紫外線更敏感。
- E與其他形式輻射相比,兩棲動物的皮膚對紫外線不那么敏感。
● 正確答案:A
收藏本題 糾錯
答案解析:
本題考查假設題型。題干結論成立必須要說明現在兩棲動物與最初的兩棲動物在紫外線承受輻射傷害方面沒有太大差異,如果現在更容易受輻射,則題干論證不成立。BC 選項為削弱,DE 選項的轉移了應該比較的兩個主體。
知識點:假設
分手不僅令人心理痛苦,還可能造成身體疼痛。美國研究人員征募 40 名志愿者,他們在過去半年中被迫與配偶分手,至今依然相當介意遭人拒絕。研究人員借助功能性磁共振成像技術觀察志愿者的大腦活動,結果發現他們對分手等社會拒絕產生反應的大腦部位與對軀體疼痛反應的部位重合,因此分手這類社會拒絕行為會引起他們軀體疼痛。上述推論隱含的假設是什么?
- A個體對于疼痛的感受與社會應激事件有密切關系。
- B功能性磁共振技術是目前進行大腦定位的常用方法。
- C個體情緒等心理過程的改變能影響其生理反應。
- D生理與心理反應可以通過大腦產生關聯。
- E生理上的痛苦總是要通過心理活動來體現。
● 正確答案:D
收藏本題 糾錯
答案解析:
D項需要假設,保證了題干的大腦部位和身體疼痛之間存在論證關聯,如果不能通過大腦關聯產生反應,那么題干的心理行為和生理之間的關系就不一定存在。
知識點:假設
“老賴”賴賬不還,不僅會造成他人的經濟利益受損,還嚴重危害社會風氣。對此,某市推出政策,將個人的“老賴”行為納入誠信檔案記錄。“老賴”行為納入誠信檔案記錄的人,其子女就讀私立學校和購買商業保險將受到限制。
要想使該項政策取得效果,必須具備的前提是:
- A一些“老賴”十分重視子女教育和風險保障
- B就讀私立學校和購買商業保險需要花費大量金錢
- C建立誠信檔案有利于打造誠信社會
- D群眾對“老賴”的所作所為深惡痛絕
- E任何政策都要關注其時效性和長效性
● 正確答案:A
收藏本題 糾錯
答案解析:
考查“必要條件”。題干論點為:通過對老賴施以限制的方式來達到減少老賴的目的。A項符合題干論點的必要條件。
知識點:假設
由污水排放掩埋帶來的污染問題在中等發達國家中最為突出,而在發達國家與不發達國家 中反而不突出。不發達國家是因為沒有多少污水排放可以處理。發達國家或者是因為有效地減 少了污水排放,或者是因為有效地處理了污水排放。W 國是中等發達國家,因此,它目前面臨 的由污水排放掩埋帶來的污染在三年后會有實質性的改變。以下哪項最可能是上述論證所假設 的?
- AW 國將在三年內成為發達國家。
- BW 國不會在三年后倒退回不發達狀態。
- CW 國將在三年內有效地處理污水排放。
- DW 國三年內保持其發展水平不變。
- EW 國將在三年內有效地減少污水排放。
● 正確答案:A
收藏本題 糾錯
答案解析:
【考點:假設】為了使得“W 國是中等發達國家,因此,它目前面臨的由污 水排放掩埋帶來的污染在三年后會有實質性的改變”。這一論證成立,最有效的參考是“ W 國將在三年內成為發達國家”。因為“發達國家或者是因為有效地減少了污水排放,或者是 因為有效地處理了污水排放。”綜上,選擇 A。
知識點:假設
跑步是目前一種流行的健身方式,但是,一項統計研究表明,一些人體器質性毛病都和跑 步有關,例如,脊椎盤錯位,足、踝扭傷,膝、腰關節磨損等。此項研究進一步表明,在剛開 始跑步鍛煉的人中,很少有這些毛病,而經常跑步的人中,多多少少都有這樣的毛病。這說明,人體扛不住經常性跑步產生的壓力。 以下哪項是上述論證所假設的?
- A經常性跑步鍛煉的人并不知道這項運動有害于身體。
- B跑步和人體的某些器質性毛病有因果關系。
- C如果不經常跑步,人體不會出現脊椎盤錯位。
- D和許多動物種類相比,人體器官對外部壓力的抵抗能力較弱。
- E應當宣傳跑步對人體有害。
● 正確答案:B
收藏本題 糾錯
答案解析:
【考點:假設】本題考察假設類題目。題干論證的是經常跑步與器質性毛病的 關系,選項 B 可搭建因果,為必要假設。
知識點:假設
超速行駛是指駕駛員在駕車行駛中,以超過法律、法規規定的速度進行行駛的行為。例如
我國高速公路的汽車行駛速度最快不超過 120km/h。有限速路交通標志或限速面標志時,應嚴格按照標志規定的速度行駛。因此,如果規定所有汽車都必須安裝一種裝置,這種裝置在汽車超速時會發出聲音提醒司機減速,那么,高速公路上的交通事故將會明顯減少。
上述論證依賴于以下哪項假設?
Ⅰ.在高速公路上超速行駛的司機,大都沒有意識到自己超速。
Ⅱ.高速公路上發生交通事故的重要原因,是司機超速行駛。
Ⅲ.上述裝置的價格十分昂貴。
- A只有Ⅰ。
- B只有Ⅱ。
- C只有Ⅲ。
- D只有Ⅰ和Ⅱ。
- EⅠ、Ⅱ和Ⅲ。
● 正確答案:D
收藏本題 糾錯
答案解析:
【考點:假設】】解析:I 必須假設,如果高速路上司機意識到超速仍超速行駛,該裝置就沒有意義了。II 必須假設,若超速行駛并非事故重要原因,即使啟用該裝置,也無法得出高速公路上的交通事故明顯減少的結論。III 與論證無關,屬于轉移論題的選項。
知識點:假設
燃料酒精是一種新能源,其優勢在于屬于可再生能源。 乙醇不僅是優良的燃料,它還是 優良的燃油品改善劑。科研人員近期研發了一種燃料酒精的新型產品:“汽油酒精”,顧名思義 是一種汽油酒精混合物。它作為一種汽車燃料,和汽油相比,燃燒一個單位的汽油酒精能產生 較多的能量,同時排出較少的有害廢氣:一氧化碳和二氧化碳。研究發現,以汽車日流量超過200 萬輛的北京市為例,如果所有汽車都使用汽油酒精,那么,每天產生的二氧化碳,不比北 京的綠色植被通過光合作用吸收得多。因此,可以預計,在世界范圍內,汽油酒精將很快進軍 并占領汽車燃料市場。 以下哪項如果為真,最可能是題干論證假設的?
- A汽車燃料產生的二氧化碳越少,越有利于提高市場占有率。
- B和汽油相比,使用汽油酒精會有利于汽車的保養。
- C使用汽油酒精將減少對汽油的需求,有利于緩解石油短缺的壓力。
- D全世界汽車日流量超過 200 萬輛的城市中,北京的綠色植被覆蓋率較低。
- E和汽油相比,汽油酒精的生產成本較低,因而售價也較低。
● 正確答案:A
收藏本題 糾錯
答案解析:
【考點:假設】答案 A。解題注意題干核心 |前提——結論| ,前端一致,后端找答案, 搭建二氧化碳和占領汽車燃料因此最“假設”是 A 選項,其他選項有加強題干的嫌疑。
知識點:假設
越來越多的人開始換購電動汽車來取代傳統的燃油車,據調查換車最主要的目的是從經濟利益考慮,電費遠比燃油便宜。然而,據一位同時開過兩類車都為5年的車主告知,同樣價格的電車和燃油車相比,總費用并沒有減少,這是因為電車5年左右由于電量衰減需要重新更換一次新電池。以上車主的說法是建立在下列哪個假設的基礎上?
- A5年后的電池更換費用與期間電費比油費省下的交通費用持平或更多。
- B車主在換電車后的行駛里程數比開燃油車時更多。
- C10年后電車的維護費用比燃油車大很多。
- D對于電動車而言,電池的價值占了整車價值的80%以上。
- E傳統燃油車由于環境污染問題將會被取代。
● 正確答案:A
收藏本題 糾錯
答案解析:
【考點:假設】解析:選項A直接是題干車主結論的支持,前提是電費比油費便宜,結論是兩類車的總花銷差不多,因此需要建立電費比油費便宜的金額至少和換電池的費用一樣的關系。其余選項無緊扣題干論述。
知識點:假設
新能源汽車的定義:因國家不同其提法也不相同,在日本通常被稱為“低公害汽車”,2001年以日本國土交通省、 環境省和經濟產業省制定了“低公害車開發普及行動計劃”。該計劃所指的低公害車包括5類,即:以天然氣為燃料的汽車、混合動力汽車、電動汽車、以甲醇為燃料的汽車、排污和燃效限制標準最嚴格的清潔汽油汽車。既然新能源汽車很有可能可以減少有害氣體的排放,那么政府就應該提供專項資金來支持測試這種可能性研究。上述陳述假設了以下哪項?
- A新能源汽車有可能減少有害氣體的排放。
- B找到減少有害氣體排放的可能性是支持政府進行此類研究的理由。
- C減少有害氣體的排放對社會有益。
- D政府是上述研究資金的唯一來源。
- E政府有充足的資金支持該研究。
● 正確答案:B
收藏本題 糾錯
答案解析:
【考點:假設】解析:B選項成立。對題干起到了完善推理,“搭橋”的作用。A重復題干,不選。C提及的社會有益沒有在題干反映,無關。D假設過于絕對,存在假設邏輯漏洞,反向思考是(這里假設選項的矛盾成立時,求證是否確實導致題干不成立,如果確實不成立,說明選項是必要的,但如果題干仍成立,則該選項不是必要的),政府如果不是資金唯一來源,有其他來源提供資金,政府也存在應該提供專項資金來同時支持研究的可能。
E選項也存在假設漏洞,反向思考是(這里假設選項成立時,求證是否確實導致題干更加完美成立,如果是,說明選項是必要的,但如果題干也存在其他的矛盾選擇,則該選項不是必要的)即使政府有充足資金,但不一定要專項支持該類研究。
知識點:假設
在20世紀50年代的一段時間,搖滾樂把爵士樂永久地趕出了音樂舞臺。證據來自那時年輕人的行為。在擁擠的夜總會中,他們熱情地為搖滾表演鼓掌,但是當爵士樂開始時,他們就出去吃冰淇淋。只有當爵士樂表演結束后他們才回來。下面哪句話,最能反駁上面的結論?
- A爵士樂是美國對于世界文化最重要的音樂貢獻。
- B盡管20世紀50年代參加夜總會的一些年輕人確實試圖聽爵士樂,他們最終對其厭煩。
- C從20世紀60年代,搖滾樂不僅為年輕人提供娛樂,而且也是社會演說時的一個振奮人心的因素。
- D盡管到1960年,爵士樂表演不那么流行,但是從那時起中產階級的職業人員中對爵士樂的興趣開始復蘇。
- E爵士樂在20世紀30年代到20世紀50年代間越來越受歡迎。
● 正確答案:D
收藏本題 糾錯
答案解析:
[答案]D
[解析]題干結論:搖滾樂把爵士樂永久地趕出了音樂舞臺。D項,如果爵士樂表演從1960年起開始在中產階級的職業人員中復蘇,那就說明在20世紀50年代,搖滾樂并沒有把爵士樂永久地趕出舞臺,削弱了題干結論。E項,時間段不符合,不能削弱。
知識點:假設
兩位大媽聽說有幫助困難學生完成學業的致遠學校。正在議論一個鄰居的孩子王小伍能否進這所學校讀書。
張大媽說:“王家的人均收入每月不足200元,這在北京來說,真夠困難的、我看王小伍能進致遠學校讀書。”
李大媽說:“我看不一定,聽說王小伍學習成績不太好,上次期末考試他有三門功課不及格呢。”
李大媽的看法如果成立,必須有以下哪項假設?
- A致遠學校只招收本地區的學生。
- B作為致遠學校的學生要品學兼優。
- C只有家庭經濟困難的學生才能進入致遠學校學習。
- D作為致遠學校的學生不一定非得家庭經濟困難。
- E僅僅家庭經濟困難,還不夠進入致遠學校學習的條件。
● 正確答案:E
收藏本題 糾錯
答案解析:
[答案]E
[解析]張大媽意思是:條件困難就能進致遠學校讀書。李大媽意思是:王小伍成績不好可能進不了致遠學校。因此,E是李大媽需要的假設。
知識點:假設
在建黨一百周年之際,今年暑假,TC國際小學合唱團來到首都北京國家大劇院為親愛的黨獻唱,孩子們深情的演唱,獲得臺下陣陣掌聲,并獲得金獎,再一次擦亮了TC的校牌。可惜,合唱團的人數過多,現領隊打算減少合唱團人數,計劃首先減少唱功相對較差的人員,而非按照其他參考因素如年齡大小、男女比例和演出費用差異等來衡量。
上述決定假定了下列哪個選項?
- A唱功差的人或許外在條件突出
- B存在能準確評判唱功能力的確切方法
- C合唱隊必須有對半的男女比例
- D不能存在兩個唱功能力幾乎一樣的人員
- E唱功差的往往演出薪資少
● 正確答案:B
收藏本題 糾錯
答案解析:
【考點:假設——方法可行】
解析:對于方法可行類的假定,首先需要假設這個方法的評判依據是切實可行的,即選項B。D容易誤選,但就算兩個唱功一樣,和其他人比也存在階梯差異,這樣一樣可以用來篩選。
知識點:假設
說到超速行駛,車主應該都不陌生。超速行駛是最常見的違法行為之一,其危害性也是相當大,據相關數據統計,每年因超速引起的交通事故達到30%。因此,如果規定所有汽車都必須安裝一種裝置,這種裝置在汽車超速時會發出聲音提醒司機減速,那么,高速公路上的交通事故將會明顯減少。
上述論證依賴于以下哪項假設
Ⅰ.在高速公路上超速行駛的司機,大都沒有意識到自己超速。
Ⅱ.高速公路上發生交通事故的重要原因,是司機超速行駛。
Ⅲ.上述裝置的價格十分昂貴。
- A只有Ⅰ
- B只有Ⅱ
- C只有Ⅲ
- D只有Ⅰ和Ⅱ
- EⅠ、Ⅱ和Ⅲ
● 正確答案:D
收藏本題 糾錯
答案解析:
I必須假設,如果高速路上司機意識到超速仍超速行駛,該裝置就沒有意義了。II必須假設,若超速行駛并非事故重要原因,即使啟用該裝置,也無法得出高速公路上的交通事故明顯減少的結論。III與論證無關,屬于轉移論題的選項。
知識點:假設
2016年1月13日國務院第119次常務會議通過,就《煙花爆竹安全管理條例》做出修訂。某評論家:官方以炮仗傷人、引起火災為理由禁止春節在城里放花炮,而不是想方設法做趨利避害的引導,這里面暗含著自覺或不自覺的文化歧視。吸煙每年致病或引起火災者,比放花炮而導致的損傷者要多得多,為何不禁?禁放花炮不僅暗含著文化歧視,而且將春節的最后一點節日氣氛清除殆盡。
以下哪項陳述是這位評論家的結論所依賴的假設?
- A諸如吃餃子、送壓歲錢等傳統節日內容在城里的春節中依然興盛不衰。
- B諸如《理想國》《黑客帝國》中的純理性人群不需要過有浪漫氣氛的節日。
- C諸如端午、中秋、重陽節等中國的傳統節日現在不是官方法定的節日。
- D諸如貼春聯、祭祖、迎送財神等烘托節日氣氛的習俗在城里的春節中已經消失。
- E社會穩定高于文化傳承。
● 正確答案:D
收藏本題 糾錯
答案解析:
解析:選項A與結論的依賴假設矛盾,其余選項為無關要素項。D選項中,題干結論是禁放花炮將春節的最后一點節日氣氛清除殆盡,注意“最后一點”“清除殆盡”,意味著除了花炮外的其他傳統節日習俗在花炮被禁止之前已經消失。
知識點:假設
開始做題