2024年7月第2周每日一練題目匯總
- 問題求解
- 條件充分性判斷
- 邏輯推理
打印試卷
問題求解
已知船在靜水中的速度為 $28\, {\rm km/h}$,河水的流速為 $2\, {\rm km/h}$,則此船在相距 $78\, {\rm km}$ 的兩地間往返一次所需時間是( ).
- A 5.9h
- B5.6h
- C5.4h
- D4.4h
- E4h
● 正確答案:B
收藏本題 糾錯
答案解析:
①船在順水中的速度為 $28+2=30$(千米/時),船在逆水中的速度為 $28-2=26$(千米/時),
②在順水中所用時間為 $\frac{78}{30}=2.6$(小時),
在逆水中所用時間為 $\frac{78}{26}=3$(小時).
③ 故兩地往返一 次所需時間為 $5.6$ 小時
【點 睛】
① 船在順水與逆水中的速度分別為 $v_{\text{船}}+v_{\text{水}}$與$v_{\text{船}}-v_{\text{水}}$.
②時間=路程/速度
知識點:行程問題
若實數$a,b,c$滿足$\left | a-3 \right |+\sqrt{3b+5}+(5c-4)^{2}=0$,則$abc$=( ).
- A-4
- B$-\frac{5}{3}$
- C$-\frac{4}{3}$
- D$\frac{4}{5}$
- E3
● 正確答案:A
收藏本題 糾錯
答案解析:
【解析】因為$\left | a-3 \right |+\sqrt{3b+5}+(5c-4)^{2}=0$,所以有$\left\lbrace\begin{array}{l} { a-3=0 } \\ { 3b+5=0 } \\ { 5c-4=0 }\end{array}\right.$.
解得$\left\lbrace\begin{array}{l} { a=3 } \\ { b=-\frac{5}{3} } \\ { c=\frac{4}{5}}\end{array}\right.$,即$abc=3\times (-\frac{5}{3})\times (\frac{4}{5})=-4$.
故本題的正確選項為A.
知識點:絕對值
某年級60年學生中,有30人參加合唱團、45人參加運動隊,其中參加合唱團而未參加運動隊的有8人,則參加運動隊而未參加合唱團的有( ).
- A15人
- B22人
- C23人
- D30人
- E37人
● 正確答案:C
收藏本題 糾錯
答案解析:
【解析】由題意,用文氏圖如下:
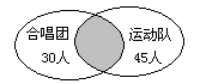
那么參加合唱團而未參加運動隊的有$30-8=22$人. 所以參加運動隊而未參加合唱團的有$45-22=23$.
故本題的正確選項為C.
知識點:集合
現有一個半徑為R的球體,擬用刨床將其加工成正方體,則能加工成的最大正方體的體積是( ).
- A$\frac{8}{3}R^{3}$
- B$\frac{8\sqrt{3}}{9}R^{3}$
- C$\frac{4}{3}R^{3}$
- D$\frac{1}{3}R^{3}$
- E$\frac{\sqrt{3}}{9}R^{3}$
● 正確答案:B
收藏本題 糾錯
答案解析:
【解析】所求最大正方體應是球的內切正方體.
設此正方體的邊長為$x$,則有$\sqrt{3}x=2R\Rightarrow x=\frac{2}{\sqrt{3}}R$.
所以正方體的體積為$V= x^{3}=\frac{8\sqrt{3}}{9}R^{3}$.
故本題的正確選項為B.
知識點:長方體
2007年某市的全年研究與試驗發展(R&D)經費支出300億元,比2006年增長20%,該市的GDP為10000億元,比2006年增長10%,2006年該市的R&D經費支出占當年GDP的( ).
- A1.75%
- B2%
- C2.5%
- D2.75%
- E3%
● 正確答案:D
收藏本題 糾錯
答案解析:
【解析】設2006年該市的R&D經費支出為$a$,2006年該市的GDP為$b$.
則根據題意有:$\left\lbrace\begin{array}{l} {a\times 1.2=300} \\ {b\times 1.1=10000}\end{array}\right.\Rightarrow\dfrac{a}{b}=\dfrac{3.3}{120}=2.75\%$.
故本題的正確選項為D.
知識點:比例問題
條件充分性判斷
$a|a-b|\geq |a|(a-b)$.
(1)實數$a> 0$.
(2)實數$a, b$滿足$a> b$.
- A條件(1)充分, 但條件(2)不充分.
- B條件(2)充分, 但條件(1)不充分.
- C條件(1)和(2)單獨都不充分,但條件(1) 和條件(2)聯合起來充分.
- D條件(1)充分, 條件(2) 也充分.
- E條件(1) 和( 2 ) 單獨都不充分 , 條件(1)和條件(2) 聯合起來也不充分.
● 正確答案:A
收藏本題 糾錯
答案解析:
法一:①條件(1):$a> 0$,則$|a|=a$,而$|a-b|\geq (a-b)$恒成立,
故$a|a-b|\geq |a|(a-b)$成立,條件(1)充分.
②條件(2):舉反例$a=-1, b=-2,$可知條件(2)不充分.
法二:①$a|a-b|\geq |a|(a-b)$
有三種情況:
I.$a=0$.
II.$a=b$.
III.$a\neq 0$且$a\neq b$時,$\frac{a}{|a|}\geq\frac{a-b}{|a-b|}\Leftrightarrow a> 0$或$a< b$,綜上,$a\geq 0$或$a\leq b$.
②對于條件(1),$a> 0$是結論的子集,故充分.
對于條件(2),$a> b$不是結論的子集,故不充分.
知識點:絕對值
有偶數位來賓.
( 1) 聚會時所有來賓都被安排坐在一張圓桌周圍, 且每位來賓與其鄰座性別不同.
( 2 ) 聚會時男賓人數是女賓人數的兩倍.
- A條件(1)充分, 但條件(2)不充分.
- B條件(2)充分, 但條件(1)不充分.
- C條件(1)和(2)單獨都不充分,但條件(1) 和條件(2)聯合起來充分.
- D條件(1)充分, 條件(2) 也充分.
- E條件(1) 和( 2 ) 單獨都不充分 , 條件(1)和條件(2) 聯合起來也不充分.
● 正確答案:A
收藏本題 糾錯
答案解析:
設男嘉賓人數為$x$,女嘉賓人數為$y$,題干要求$x+y$為偶數.
由條件(1),必有$x=y$,因此$x+y=2x$為偶數,所以條件(1)充分.
由條件(2),有$x=2y$,因此$x+y=3y$不一定為偶數,所以條件(2)不充分.
知識點:質數、合數和奇數、偶數
售出一件甲商品比售出一件乙商品利潤要高.
(1 ) 售出5 件甲商品,4 件乙商品共獲利50 元 .
( 2 ) 售出 4 件甲商品,5 件乙商品共獲利47 元.
- A條件(1)充分, 但條件(2)不充分.
- B條件(2)充分, 但條件(1)不充分.
- C條件(1)和(2)單獨都不充分,但條件(1) 和條件(2)聯合起來充分.
- D條件(1)充分, 條件(2) 也充分.
- E條件(1) 和( 2 ) 單獨都不充分 , 條件(1)和條件(2) 聯合起來也不充分.
● 正確答案:C
收藏本題 糾錯
答案解析:
設甲每件利潤為$x$元,乙每件利潤為$y$元,題干要求推出$x> y$.
條件(1)和條件(2)單獨顯然不充分.
聯合起來有:$\left\lbrace\begin{array}{l} {5x+4y=50} \\ {4x+5y=47}\end{array}\right.$即$x-y=3$,所以$x> y$成立.
知識點:方程組問題
已知數列$\left \{a_{n} \right \}$為等差數列,公差為d , $a_{1} + a_{2} + a_{3} + a_{4} = 12 $ , 則 $a_{4} = 0$
(1)d = - 2。
(2)$a_{2} + a_{4} = 4$
- A條件(1)充分, 但條件(2)不充分.
- B條件(2)充分, 但條件(1)不充分.
- C條件(1)和(2)單獨都不充分,但條件(1) 和條件(2)聯合起來充分.
- D條件(1)充分, 條件(2) 也充分.
- E條件(1) 和( 2 ) 單獨都不充分 , 條件(1)和條件(2) 聯合起來也不充分.
● 正確答案:D
收藏本題 糾錯
答案解析:
設此等差數列的首項為a1,公差為d.
題干中給出$a _ { 1 } + a _ { 2 } + a _ { 3 } + a _ { 4 } = 1 2 \Rightarrow 4 a _ { 1 } + 6 d = 1 2 \Rightarrow 2 a _ { 1 } + 3 d = 6 . $
即$2 a _ { 1 } + 3 d = 6 . $
由條件(1),有$\left\lbrace\begin{array}{l} { 2 a _ { 1 } + 3 d = 6 } \\ { d = - 2 } \end{array}\right. ,$ 解得$a _ { 1 } = 6 $.所以$a _ { 4 } = a _ { 1 } + 3 d = 6 + 3 \cdot ( - 2 ) = 0 . $
所以條件(1)充分.
由條件(2),有$\left\lbrace\begin{array}{l} { 2 a _ { 1 } + 3 d = 6 } \\ { a _ { 1 } + d + a _ { 1 } + 3 d = 4 } \end{array}\right. \Rightarrow \left\lbrace\begin{array}{l} { a _ { 1 } = 6 } \\ { d = - 2 } \end{array}\right. $ 所以$a _ { 4 } = a _ { 1 } + 3 d = 6 + 3 \cdot ( - 2 ) = 0 . $
所以條件(2)充分.
知識點:等差數列
甲企業今年人均成本是去年的60%.
(1 ) 甲企業今年總成本比去年減少 25% ,員工人數增加25%.
( 2 ) 甲企業今年總成本比去年減少 28% ,員工人數增加20%.
- A條件(1)充分, 但條件(2)不充分.
- B條件(2)充分, 但條件(1)不充分.
- C條件(1)和(2)單獨都不充分,但條件(1) 和條件(2)聯合起來充分.
- D條件(1)充分, 條件(2) 也充分.
- E條件(1) 和( 2 ) 單獨都不充分 , 條件(1)和條件(2) 聯合起來也不充分.
● 正確答案:D
收藏本題 糾錯
答案解析:
設去年總成本為a,總人數為b.
由條件(1)有 $\frac { a ( 1 - 2 5 \% ) } { b ( 1 + 2 5 \% ) } = \frac { a } { b } \times 6 0 \% . $ 所以條件(1)充分.
由條件(2)有 $\frac { a ( 1 - 2 8 \% ) } { b ( 1 + 2 0 \% ) } = \frac { a } { b } \times 6 0 \% . $所以條件(2)充分.
知識點:比例問題
該股票漲了.
(1)某股票連續三天漲10%后, 又連續三天跌 10%.
(2)某股票連續三天跌 10%后, 又連續三天漲10%.
- A條件(1)充分, 但條件(2)不充分.
- B條件(2)充分, 但條件(1)不充分.
- C條件(1)和(2)單獨都不充分,但條件(1) 和條件(2)聯合起來充分.
- D條件(1)充分, 條件(2) 也充分.
- E條件(1) 和( 2 ) 單獨都不充分 , 條件(1)和條件(2) 聯合起來也不充分.
● 正確答案:E
收藏本題 糾錯
答案解析:
設該股票的原價為a,現價為b.
由條件(1),$b = a ( 1 + 0 . 1 ) ^ { 3 } ( 1 - 0 . 1 ) ^ { 3 } = a ( 1 - 0 . 0 1 ) ^ { 3 } < a . $所以條件(1)不充分.
由條件(2),$b = a ( 1 - 0 . 1 ) ^ { 3 } ( 1 + 0 . 1 ) ^ { 3 } = a ( 1 - 0 . 0 1 ) ^ { 3 } < a . $所以條件(2)不充分.
條件(1)和條件(2)沒有辦法聯合,所以本題的正確選項為E.
知識點:比例問題
某班有50 名學生, 其中女生26 名, 已知在某次選拔測試中 ,有 27 名學生未通過, 則有 9 名男生通過.
(1) 在通過的學生中,女生比男生多 5 人.
(2) 在男生中,未通過的人數比通過的人數多 6 人.
- A條件(1)充分, 但條件(2)不充分.
- B條件(2)充分, 但條件(1)不充分.
- C條件(1)和(2)單獨都不充分,但條件(1) 和條件(2)聯合起來充分.
- D條件(1)充分, 條件(2) 也充分.
- E條件(1) 和( 2 ) 單獨都不充分 , 條件(1)和條件(2) 聯合起來也不充分.
● 正確答案:D
收藏本題 糾錯
答案解析:
①設通過的男生人數為 $x$ 人.
條件(1):$x+(x+5)=50-27\Rightarrow x=9$,故條件(1)充分.
②條件(2):$x+(x+6)=50-26\Rightarrow x=9$,故條件(2)也充分.
【點睛】當題目中有多個未知量,且已知未知量之間的關系時,可根據未知量的關系方程,最后解出未知量.
知識點:其他問題
甲企業一年的總產值為 $\frac{a}{p}\lbrack (1+p)^{12}-1\rbrack.$
(1) 甲企業一月份的產值為 $a$ , 以后每月產值的增長率為 $p$.
(2) 甲企業一月份的產值為 $\frac{a}{2}$,以后每月產值的增長率為 $2p$.
- A條件(1)充分, 但條件(2)不充分.
- B條件(2)充分, 但條件(1)不充分.
- C條件(1)和(2)單獨都不充分,但條件(1) 和條件(2)聯合起來充分.
- D條件(1)充分, 條件(2) 也充分.
- E條件(1) 和( 2 ) 單獨都不充分 , 條件(1)和條件(2) 聯合起來也不充分.
● 正確答案:A
收藏本題 糾錯
答案解析:
由條件(1),甲1月份的產值為 $a$,則2月份為 $a(1+p)$,3月份為 $a(1+p)^{2}$,...12月份為 $a(1+p)^{11}$.
所以一年的總產值為:
$a+a(1+p)+a(1+p)^{2}+\cdots +a(1+p)^{11}=a\cdot\frac{1-(1+p)^{12}}{1-(1+p)}=\frac{a}{p}\lbrack (1+p)^{12}-1\rbrack.$
即條件(1)是充分的.
由條件(2),一年的總產值為:
$\frac{a}{2}+\frac{a}{2}(1+2p)+\frac{a}{2}(1+2p)^{2}+\cdots +\frac{a}{2}(1+2p)^{11}=\frac{a}{2}\cdot\frac{1-(1+2p)^{12}}{1-(1+2p)}=\frac{a}{2}\cdot\frac{1}{2p}\lbrack (1+2p)^{12}-1\rbrack$
所以條件(2)不充分.
知識點:等比數列
設 a , b 為非負實數, 則$a+b \leq \frac{5}{4}$
(1)$ab \leq \frac{1}{16}$
(2)$a^{2}+b^{2}\leq 1$
- A條件(1)充分, 但條件(2)不充分.
- B條件(2)充分, 但條件(1)不充分.
- C條件(1)和(2)單獨都不充分,但條件(1) 和條件(2)聯合起來充分.
- D條件(1)充分, 條件(2) 也充分.
- E條件(1) 和( 2 ) 單獨都不充分 , 條件(1)和條件(2) 聯合起來也不充分.
● 正確答案:C
收藏本題 糾錯
答案解析:
①條件(1):舉反例a=100,$b = \frac{1}{1600}$,可知條件(1)不充分.
②條件(2):舉反例$a = b = \frac{\sqrt{2}}{2}$,可知條件(2)不充分.
③聯合條件(1)和條件(2):$\left\lbrace\begin{array}{l} { a b \leq \frac { 1 } { 1 6 } } \\ { a ^ { 2 } + b ^ { 2 } \leq 1 } \end{array}\right. \Rightarrow \left\lbrace\begin{array}{l} { 2 a b \leq \frac { 1 } { 8 } } \\ { a ^ { 2 } + b ^ { 2 } \leq 1 } \end{array}\right. $,
$\Rightarrow a ^ { 2 } + 2 a b + b ^ { 2 } = ( a + b ) ^ { 2 } \leq \frac { 1 } { 8 } + 1 = \frac { 9 } { 8 } , $
又a,b≥0,故$a + b \leq \sqrt { \frac { 9 } { 8 } } = \frac { 3 \sqrt { 2 } } { 4 } < \frac { 5 } { 4 } , $聯合充分.
知識點:不等式
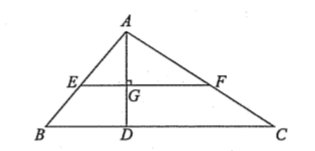
如圖所示, 在△ABC 中, 已知EF∥BC, 則△AEF的面積等于梯形 EBCF的面積.
(1)|AG|=2|GD|
(2)|BC|=$\sqrt{2}$|EF|
- A條件(1)充分, 但條件(2)不充分.
- B條件(2)充分, 但條件(1)不充分.
- C條件(1)和(2)單獨都不充分,但條件(1) 和條件(2)聯合起來充分.
- D條件(1)充分, 條件(2) 也充分.
- E條件(1) 和( 2 ) 單獨都不充分 , 條件(1)和條件(2) 聯合起來也不充分.
● 正確答案:B
收藏本題 糾錯
答案解析:
①條件(1):$\triangle AEF\sim \triangle ABC$又$\frac { | A G | } { | A D | } = \frac { 2 } { 3 } $,
即相似比為2:3,所以面積之比為4:9,
故$S_{\triangle AEF}:S_{BCFE}=4:5$,所以$\triangle AEF$的面積不等于梯形的面積,
條件(1)不充分.
②條件(2):$\triangle AEF\sim \triangle ABC$又$\frac { | E F| } { | B C | } = \frac { 1 } { \sqrt{2} } $,故$\frac { S _ { \triangle A E F } } { S _ { \triangle A B C } } = \frac { 1 } { 2 } , $
所以S△AEF:S四邊形BCFE=1:1,所以$\triangle AEF$的面積等于梯形的面積,
條件(2)充分.
【點睛】若兩個三角形相似,則兩三角形對應的邊長之比等于兩三角形的相似比;兩三角形的面積之比等于兩三角形相似比的平方.
知識點:三角形
邏輯推理
小明、小紅、小麗、小強、小梅五人去聽音樂會,他們五人在同一排且座位相連,其中只有一個座位最靠近走廊,結果小強想坐在最靠近走廊的座位上,小麗想跟小明緊挨著,小紅不想跟小麗緊挨,小梅想跟小麗緊挨著,但不想跟小強或小明緊挨著。
以下哪項順序符合上述五人的意愿?
- A小明,小梅,小麗,小紅,小強。
- B小強,小紅 ,小明,小麗,小梅。
- C小強,小梅,小紅,小麗,小明。
- D小明,小紅,小梅,小麗,小強。
- E小強,小麗,小梅,小明,小紅。
● 正確答案:B
收藏本題 糾錯
答案解析:
【提示】考生可采用代入排除法快速解題。
①小強想坐在最靠近走廊的座位上。②小麗想跟小明緊挨著。
③小紅不想跟小麗緊挨著。
④小梅想跟小麗緊挨著,不想跟小強或小明緊挨著。
由②可知小麗跟小明在一起 , 淘汰 A、D。
由③可知小麗跟小紅不挨產, 淘汰 C。
由④小梅不想跟 小明緊挨著, 淘汰 E。答案選B。
知識點:排序分組
參加某國際學術研討會的60 名學者中,亞裔學者 31人,博士33人,非亞裔學者中無博士學位的4 人。
根據上述陳述,參加此次國際研討會的亞裔博士有幾人?
- A1 人。
- B2 人。
- C4 人。
- D 7 人。
- E 8 人。
● 正確答案:E
收藏本題 糾錯
答案解析:
【解題關鍵】數據分析問題,緊扣數據之間的交叉關系即可。
① 60 名學者是總數。
②31 個亞裔學者, 33 個博 士。
③亞裔學者中無博士學位的四人。
由②可知: 非亞裔學者為29人,無博士學位的是27人, 非亞裔學者中有博士學
位的25人, 亞裔學者中無博士學位的23人。
由亞裔學者一共有31個,可知有8 個人既是亞裔學者,又是博士。
知識點:其他推理
對某高校本科生的某項調查統計發現:在因成績優異被推薦免試攻讀碩士研究生的文科專業學生中,女生占有70%,由此可見,該校本科文科專業的女生比男生優秀。
以下哪項如果為真,能最有力地削弱上述結論?
- A在該校本科文科專業學生中,女生占30% 以上。
- B在該校本科文科專業學生中,女生占30%以下。
- C在該校本科文科專業學生中,男生占30%以下。
- D在該校本科文科專業學生中 ,女生占70%以下。
- E在該校本科文科專業學生中,男生占70%以上。
● 正確答案:C
收藏本題 糾錯
答案解析:
本題屬于典型的同比削弱差比加強的問題,依據女生占整個文科專業的比例超過、接近、等于70%即可快速解題。
被推薦免試讀研的文科專業考生中,女生占70%→該校本科生專業的女生比男生優秀:
A 女生占30%以上,可能削弱結論,但是力度不強,只有女生比例占到70%以上才是較強的削弱。B 女生占30%以下,正好說明女生比男生優秀,女生推薦免試讀研的比例比男生推薦免試讀研的比例高,支持了結論。C 男生占30%以下,說明女生比例占到了70%以上,女生比例占到了70%以上,推薦免試讀研的比例70%,說明該校男生比女生優秀,削弱了結論。D 男生占30%以上,說明女生占比例70%以下,支持了結論。E 男生占70%以上,說明女生占30%以下,正好得出女生比男生優秀,女生推薦免試讀研的比例比男生推薦免試讀研的比例高,支持了結論。
知識點:削弱
某中藥配方有如下要求:
(1) 如果有甲藥材,那么也要有乙藥材;
(2) 如果沒有丙藥材,那么必須有丁藥材;
(3) 人參和天麻不能都有;
(4) 如果沒有甲藥材而有丙藥材,則需 要有人參。如果含有天麻,則關于該配方的斷定哪項為真?
- A含有甲藥材。
- B含有丙藥材。
- C沒有丙藥材。
- D沒有乙藥材和丁藥材。
- E含有乙藥材或丁藥材。
● 正確答案:E
收藏本題 糾錯
答案解析:
① 甲藥材 → 乙藥材。
②沒有丙藥材 →丁藥材。
③沒有天麻∨沒有人參 =天麻 →沒有人參 。
④沒有甲藥材∧ 丙藥材→有人參。
⑤有天麻。
由⑤和③可知:有天麻,一定沒有人參。
由沒有人參退出,或者有甲藥材,或者沒有丙藥材。
由有甲藥材推出有乙藥材,沒有丙藥材推出有丁藥材。由此可知:或者有乙藥材,或者有丁藥材。
知識點:復合推理
陳先生:未經許可侵入別人的計算機,就好像開偷來的汽車撞傷了人,這些都是犯罪行為。但后者性質更嚴重,因為它既侵占了有形財產,又造成了人身傷害:而前者只是在虛擬世界中搗亂。
林女士:我不同意。例如,非法侵入醫院的計算機,有可能擾亂醫療數據,甚至危及病人的生命。因此,非法侵入計算機同樣會造成人身傷害。
以下哪項最為準確地概括了兩人爭論的焦點?
- A非法侵入別人計算機和開偷未的汽車是否同樣會危及人的生命?
- B非法侵入別人計算機和開偷來的汽車傷人是否同樣構成犯罪?
- C非法侵入別人計算機和開偷來的汽車傷人是否是同樣性質的犯罪?
- D非法侵入別人計算機犯罪性質是否和開偷來的汽車傷人一樣的嚴重?
- E是否只有侵占有形財產才構成犯罪?
● 正確答案:D
收藏本題 糾錯
答案解析:
【提示】考生需明確核心詞“性質嚴重”是二者爭論的焦點。
陳先生:未經許可入侵別人的計算機只在虛擬世界中搗亂,沒有造成人身傷害。性質不如開偷來的汽車撞人的性質嚴重。
林女士:非法入侵別人的計算機也同樣會造成人身傷害,性質跟開偷來的汽車性質一樣嚴重。
二者爭論的焦點顯 然是性質的嚴重程度是否是等同的。答案選 D。(考生抓住核
心詞可以快選。)
知識點:評價
在本年度籃球聯賽中,長江隊主教練發現,黃河隊五名主力隊員之間的上場配置有如下規律:
( 1 ) 若 甲上場, 則乙也要上場;
( 2 ) 只有甲不上場,丙才不上場;
( 3 ) 要么丙不上場,要么乙和戊中有人不上場;
( 4 ) 除 非丙不上場,否則丁上場。
若乙不上場,則以下哪項配置合乎上述規律?
- A甲、丙、丁同時上場。
- B丙不上場 ,丁、戊同時上場。
- C甲不上場,丙,丁都上場。
- D甲、丁 都上場,戊不上場。
- E甲、丁、戊都不上場。
● 正確答案:C
收藏本題 糾錯
答案解析:
①甲上場 →乙上場。
②丙不上場→甲不上場=甲上場→丙上場。 ③要么丙不上場,要么乙和戊中有人不上場。
@丁不上場→丙不上場。
由于乙不上場 , 根據①則可推出,甲不上場。
由③可知:乙不上場為真,則乙和戊中有人不上場為真,根據不相容選言判斷
,規則,肯定一個可推出否定另一個可知丙上場。
根據④, 丙上場可得出丁上場 ,由此可知,甲不上場, 丙、丁都上場, 答案選C。
知識點:復合推理
S市環保檢測中心的統計分析表明,2009年空氣質量為優的天數為150天,比2008 年多出22 天。二氧化碳、一氧化碳、二氧化氮、可吸入顆粒物四項污染物濃度平均值,與2008 年相比分別下降了約21. 3% 、25. 6% 、26. 2% 、15. 4% 。S 市環保負責人指出,這得益于近年來本市政府持續采取的控制大氣污染的相關措施。
以下除哪項外,均能支持上述S市環保負責人的看法?
- AS市廣泛展開環保宣傳, 加強了市民的生態理念和環保意識。
- Bs市啟動了內部控制污染方案 ;凡是排放不達標的燃煤鍋爐停止運行。
- CS市執行了機動車排放國 W標準,單車排放比皿標準降低了49% 。
- DS市市長辦公室最近研究了焚燒秸秤的問題,并著手制定相關條例。
- Es市制定了“綠 色企業”標準,繼續加快污染重、能耗高的企業的退出。
● 正確答案:D
收藏本題 糾錯
答案解析:
【提示】題干論證為:空氣質量改善得益于政府的措施,考生試想,得益于表示政府的措施是“因“,而空氣質量改善是“果”,那么必須保證”因“發生,即措施實施才行,因此可快速判定D 選項為正確答案,因為“著手制定” 還沒發生呢。
采取控制大氣污染的措施→空氣質量改善
A 開展環保宣傳,采取了措施。
B 啟動內部控制污染方案,采取了措施。
C 執行了標準,采取了措施。
D 著手制定相關條例,并沒有采取具體措施。
E 制定了標準,采取了相關措施。
知識點:加強
在某次思維訓練課上,張老師提出“尚左數”這一概念的定義:在連續排列的一組數字中,如果一個數字左邊的數字都比其大(或無數字),且其右邊的數字都比其小(或無數字),則稱這個數字為尚左數。
根據張老師的定義,在 8 9 7 6 4 5 3 2 這列數字中,以下哪項包含了該列數字中所有的尚左數?
- A4、5、7 和 9。
- B2、3、6 和 7。
- C 3、6、7 和 8。
- D 5、6、7 和 8。
- E2、3、6 和 8。
● 正確答案:B
收藏本題 糾錯
答案解析:
尚左數定義為:左邊的數字都比它大 ∧右邊的數字都比它小。
顯然可以看出 7、6 應該是屬于這個定義,排除A、E。顯然8不是屬于這個定義,排除C、D, 答案選B。
知識點:概念考點
一般認為,劍乳齒象是從北美洲遷入南美洲的。劍乳齒象的顯著特征是具有較直的長劍型門齒,顆骨較短,臼齒的齒冠隆起,齒板數目為7至8個,并呈乳狀突起,劍乳齒象因此得名。劍乳齒象的牙齒比較復雜,這表明它能吃草,在南美洲的許多地方都有證據顯示史前人類捕 捉過劍乳齒象。由此可以推測,劍乳齒象的滅絕可能與人類的過度捕殺有密切關系。
以下哪項如果為真,最能反駁上述結論?
- A史前動物之間經常發生大規模相互捕殺的現象。
- B劍乳齒象在遇到人類攻擊時缺乏 自我保護能力。
- C劍乳齒象也存在由南美洲 進入北美洲的回遷現象。
- D由于人類活動范圍的擴大,大型食草動物難以生存。
- E幼年劍乳齒象的牙齒結構比較簡單,自我生存能力弱。
● 正確答案:A
收藏本題 糾錯
答案解析:
人類過度捕殺→劍乳齒象滅絕
A 說明可能不是由于人類過度捕殺導致的劍乳齒象滅絕,而是由于史前動物間的互相殘殺, 存在他因。
B 部分支持了題干論證,說明是由于人類過度捕殺導致的滅絕,存在可能性。
正確淘汰
C 考生注意“也存在”=“有的”,其反駁力度較弱,好好體會一下。
D “人類活動”包含“人類捕殺”,部分支持題干。
E 該項欲構建幼年劍乳齒象自我生存能力弱→滅絕這一論證關系,從而削弱題干論證關系,考生誤將其作為“他因”思路削弱題干。
其實選項信息與題干結論構不成因果關系。所有動物幼年生存能力都弱,但為何有的沒滅絕?有這個“因“,可能導致果,也可能不導致果,說明因果無關。
知識點:削弱
小東在玩“勇士大戰”游戲,進入第二關時,界面出現四個選項。第一個選項是“選擇任意選項都需要支付游戲幣",第二個選項是”選擇本項后可以得到額外游戲獎勵",第三個選項是”選擇本項游戲后游戲不會進行下去",第四個選項是“選擇某個選項不需要支付游戲幣”。
如果四個選項中的陳述只有一句為真,則以下哪項一定為真?
- A所有選項都需支付游戲幣
- B選擇任意選項都不需要支付游戲幣。
- C選擇任意選項都不能得到額外游戲獎勵。
- D選擇笫二個選項后可以得到額外游戲獎勵。
- E選擇笫三個選項后游戲能繼續進行下去。
● 正確答案:E
收藏本題 糾錯
答案解析:
①所有選項都需支付游戲幣。
②第二個選項可以獲得額外游戲獎勵。③第三個選項游戲不會繼續。
④有的選項不需要支付游戲幣。
顯然①和④矛盾, 必有一真一假; 因此②和③必然為假。(考生注意:①和④的
真假關系無法判斷,理解一下。)
②若為假,則選擇笫二個選項不會獲得額外的游戲獎勵;③若為假,則選擇笫三個選項后 游戲會繼續進行下去,由此可知,答案選E。
知識點:真假話推理
有位美國學者做了一個實驗,給被試兒童看三幅圖畫:雞、牛、青草,然后讓兒童將其分為兩類。結果大部分中國兒童把牛和青草歸為一類,把雞歸為另一類;大部分美國兒童則把牛和雞歸為一類,把青草歸為另一類。這位美國學者由此得出:中國兒童習慣千按照事物之間的關系來分類,美國兒童則習慣于把事物按照各自所屬的“實體”范疇進行分類。
以下哪項是這些學者得出結論所必須假設的?
- A馬和青草是按照事物之間的關系被列為一類。
- B鴨和雞蛋是按照各自所屬的實體范疇被歸為一類。
- C美國兒童 只要把牛和雞歸為一類,就是習慣于 按照各自所 屬實體范疇進行分類。
- D美國兒童只要把牛和雞歸為一類,就不是習慣于按照事物之間的關 系來分類。
- E中國兒童只要把牛和青草歸為一類 ,就不是習慣于 按照各自所 屬實體范疇進行分類。
● 正確答案:C
收藏本題 糾錯
答案解析:
本題存在以下兩個假設,考生好好分析一下:
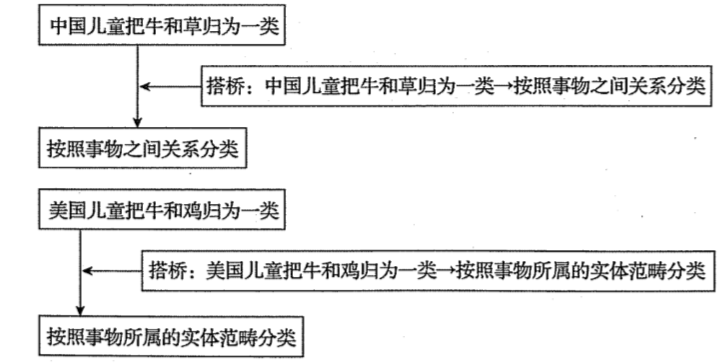
知識點:假設
相互尊重是相互理解的基礎,相互理解是相互信任的前提;在人與人的相互交往中, 自重、自信也是非常重要的,沒有一個人尊重不自重的人,沒有一個人信任他所不尊重的人。
以上陳述可以推出以下哪項結論?
- A不自重的人也不被任何人信任。
- B相互信任才能 相互尊重。
- C不自信的人也不自重。
- D不自信的人也不被任何人信任。
- E不自信的人也不受任何人尊重。
● 正確答案:A
收藏本題 糾錯
答案解析:
【提示】題干不涉及不自信的人,快速排除 C、D 、E 三個選項, 根據Q 是 P 的基礎, 可得B選項肯定Q 什么也推不出, 答案選A。
①相互尊重是相互理解的基礎,即:Q是P的基礎, 相互理解→相互尊重; 相互理解是相互信任的前提,即: Q 是 P 的前提。相互信任→相互理解。
②所有人都不尊重不自重的人。不尊重→不自重的人。
③所有人都不信任他所不尊重的人。不信任→不尊重的人。
A ②和③可以推出結論為所有人都不信任不自重的人,恰好與 A 選項相符合。
B 由①可知, 相互信任→相互尊重,選項條件關系顯然與題干不一致。
C 題干中并不涉及自信(題干是信任)與自重之間的關系。
D 題干不涉及自信與被信任之間的關系。
E 題干不涉及自信與被尊重之間的關系。
知識點:直言判斷(命題)
學生:IQ 和 EQ 哪個更重要?您能否給我指點一下?
學長:你去書店問問工作人員關于IQ 和 EQ 的書, 哪類銷得快,哪類就更重要。以下哪項與上述題千中的問答方式最為相似?
- A員工:我們正制定一個度假方案,你說是在本市好,還是去外地好? 經理:現在年終了,各公司都在安排出去旅游,你去問問其他公司的同行,他們計劃去哪里,我們就不去哪里,不湊熱鬧。
- B平平:母親節那天我準備給媽媽送一份禮物,你說是送花好還是巧克力好?佳佳:你在母親節前一天去花店看一下,看看買花的人多不多就行了嘛。
- C顧客:我準備買一件毛衣,你看顏色是 鮮艷一點,還是素一點好? 店員:這個需要結合自己的性格與穿衣習慣,各人可以有自己的選擇與喜好。
- D游客:我們前面有兩條山路 ,走哪一條更好? 導游:你仔細看看,哪一條山路上車馬的痕跡深,我們就走哪一條。
- EE.學生:我正在準備期末復習,是做教材上的練習重要,還是理解教材內容更重要? 老師:你去問問高年級得分高的同學,他們是否經常背書做練習。
● 正確答案:D
收藏本題 糾錯
答案解析:
學生: A 或B 哪個更重要?
學長: A 與B 哪個受關注度高, 哪個就更重要。
A 選項A 與 B 哪個受關注度高,關注度大的反而不去,與題干不符。B 沒有提及A 與 B 之間的 關系。
C 各個人的喜好不同,沒有說明受關注度對于A 與 B 的影響。
D A 與 B 相比,車馬的痕跡哪個深,就選哪個,與題干論證方式相同。 E 沒有提及A與B的關系。
知識點:其他推理
李赫、張嵐、林宏、何柏、邱輝5 位同事, 近日他們各自買了一臺不同品牌小轎 車,分 別為雪鐵龍、奧迪、寶馬、奔馳、桑塔納。這五輛車的顏色分別與 5 人名字最后一個字諧音的顏色不同。已知李赫買的是藍色的雪鐵龍。
以下哪項排列可能依次對應張嵐、林宏、何柏、邱輝所買的車?
- A灰色奧迪、白色寶 馬、灰色奔馳、紅色桑塔納
- B黑色奧迪、紅色寶馬、灰色奔馳、白色桑塔納
- C紅色奧迪、灰色寶 馬、白色奔 馳、黑色桑塔納
- D白色奧迪、黑色寶 馬、紅色奔馳、灰色桑塔納
- E黑色奧迪、灰色寶 馬、白色奔馳、紅色桑塔納
● 正確答案:A
收藏本題 糾錯
答案解析:
【提示】考生可采用代入排除法快速解題。
①五輛車的顏色與5 人名字最后一個字諧音的顏色不同。②李赫買的是藍色雪鐵龍。
林宏不能買紅色的車, 淘汰 B 選項。
何柏不能買白色的車,淘 汰 C、E 選項。
邱輝不能買灰色的車, 淘汰 D 選項。得出答案選A。
知識點:組合排列
克魯特是德國家喻戶曉的“明星“北極熊,北極熊是名副其實的北極霸主,因此,克魯特是名副其實的北極霸主。
以下哪項除外,均與上述論證中出現的謬誤相似?
- A兒童是祖國的花朵,小雅是兒童,因此,小雅是祖國的花朵。
- B魯迅的作品不是一天能讀完的 ,《祝福》是魯迅的作品,因此《 祝福》不是一天能讀完的。
- C中國人是不怕困難的,我是中國人,因此 ,我是不怕困難的。
- D康怡花園坐落在清水街, 清水街的建筑屬于違章 建筑,因此,康怡花園的建筑屬于違章建筑。
- E西班牙是外語,外語是普通高等學校招生的必考科目,因此西班牙語是普通高等學校招生的必考科目。
● 正確答案:D
收藏本題 糾錯
答案解析:
【提示】判斷選項屬于集合概念和非集合概念是關鍵,“清水街的建筑是違章建筑”可得出: 清水街的每一棟建筑都違章,因此D 選項推理是正確的。
題干論證中“明星“北極熊特指的是克魯特,而后北極熊指的是整體。顯然偷換概念。
A 祖國的花朵這個概念在前是指兒童,后面是指小雅,顯然偷換了概念。
B 魯迅的作品這個概念在前指全部的作品,后面指《祝福》,顯然偷換了概念。
C 中國人這個概念在前指全國的人,后面是指我自己,顯然偷換了概念。
淘汰
D 康怡花園在此的內涵和外延是一致的。
E 西班牙語是外語的一種,未必所有的外語都是西班牙語,偷換概念。
知識點:概念考點
開始做題